
在中考试卷中有一类二次函数背景下的存在性问题,比如,二次函数背景下的特殊三角形存在性问题,特殊四边形存在性问题.本讲就二次函数背景下平行四边形存在性问题的解法作一详细的探究,以期同学们心领神会,中考时再多得几分.
二次函数背景下平行四边形存在性问题常见的有三类,一类是,三定一动型(较易),另一类是,两定两动型(较难且常考),还有一类是,一定三动型(难而少见).本讲以一例中考题对第第二类进行探究.
【题目呈现】
☞如图,抛物线y=一x² bx c与x轴分别交于A(一1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,连接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点,试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.

【分析】(1)较易,只须将A,B两点坐标代入抛物线的解析式,解方程组即可,得b=4,c=5,∴抛物线的解析式为y=一x² 4x 5.
(2)∵AD=5,且OA=1,∴OD=6,又CD=8,∴C(一6,8),设平移后点C的对应点为C',则C'点的纵坐标为8,代入抛物线解析式可得8=一x² 4x 5,解得x=1或x=3,∴C'点的坐标为(1,8)或(3,8),∴当点C落在抛物线上时,向右平移了7或9个单位,∴m的值为7或9.
(3)是本题的重点,坐标系下的问题一般有三类解法,一是,纯几何解法,根据条件运用几何有关定理,推论,推证出问题;二是,纯代数解法,设出点的坐标,依据条件列出方程,解出结果;三是,几何代数混合解法。三种解法各有特点,混合解法往往优缺互补,为大多人所喜好,当然,对于不同的题目,同学们应具体分析,使用最简捷的方法。
※几何代数混合解法
首先求出抛物线的对称轴为直线x=2,由于点P在对称轴上运动,可设P(2,t),由(2)可知E点坐标为(1,8),点Q在抛物线上,可设Q(x,y),因E,B两点确定,采取抓不变量的策略,以不变应万变,为实现以静制动的目的,需分类讨论:
①当BE为平行四边形的边时,记BE交对称轴于点M,过E作EF⊥x轴于点F,此时PQ也为平行四边形的边,过Q作对称轴的垂线,垂足为N,如图.(另一种情况用红线标出).
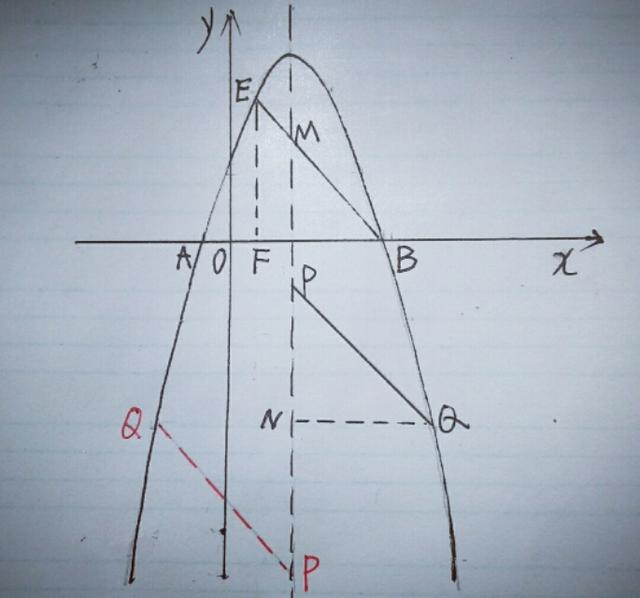
易知∠BEF=∠BMP=∠QPN,∠PNQ=∠EFB=90°,PQ=BE,∴△PQN≌△EBF,∴NQ=BF=OB一OF=4,这时我们注意PQ做边时有两种情况,为了简化运用,或者说不明确点Q在对称轴的哪一方时,用绝对值表示NQ的长可避免繁琐的讨论,则NQ=|x一2|=4,解得x=一2或x=6,当x=一2或x=6时代入抛物线的解析式可得y=一7,∴Q点坐标为(一2,一7)或(6,一7);
②当BE为平行四边形的对角线时,PQ也为平行四边形的对角线,线段BE的中点D也为线段PQ的中点,∵B(5,0),E(1,8),∴中点D的坐标为(3,4),∴x 2=3×2,解得x=4,把x=4代入抛物线的解析式,得y=5,∴Q(4,5),如图,

综上可知,Q点的坐标为(一2,一7)或(6,一7)或(4,5).
※平移法
我们知道,在平移变换中,只改变图形的位置,不改变图形的大小,且对应点的连线平行(或在一直线上),而平行四边形对边平行且相等,可看成一条线段按某一方向平移一定的距离而形成,线段平移后形成平行四边形的对边,线段的两端点与其对应点的连线段形成平行四边形的另一组对边,基于此,
当EB做平行四边形的边时,试着平移EB,可得到两种情况的平行四边形,如下图的(1)与(2),(简化图)

如图(1),点E(1,8)平移到点B(5,0)时,向右平移4个单位,向下平移8个单位,则点P(2,t)也作同样的平移变换到点Q(x,y),则2 4=x,(这里只求点Q的横坐标),代入函数解析式可求得点Q的纵坐标y=一7,∴点Q(6,一7).
如图(2),点E(1,8)平移到点B(5,0)时,向右平移4个单位,向下平移8个单位,则点Q(x,y)也作同样的平移变换到点P(2,t),则x 4=2,∴x=一2(这里只求点Q的横坐标),代入函数解析式可求得点Q的纵坐标y=一7,∴点Q(一2,一7).
当BE做对角线时,仿照几何代数混合解法求得点Q的坐标(4,5).如上图(3).
※代数法
我们知道平行四边形的对角线互相平分,一条对角线的中点也是另一条对角线的中点,如图

在平行四边形ABCD中,设A点坐标为(xA,yA),B点坐标为(xB,yB),C点坐标为(xC,yC),D点坐标为(xD,yD),由中点坐标公式可得,xO=(xA xC)/2=(xB xD)/2,yO=(yA yC)/2=(yB yD)/2,即xA xC=xB xD,yA yC=yB yD,这是通用的两个公式,若知三点坐标可求第四点的坐标,通过上面的解法发现,抓住某一点分别与其余三点连线为对角线,可以不重不漏地分类所有情况,所以,
①当EB做对角线时,PQ也为对角线,则,xE xB=xP xQ,即1 5=2 xQ,得xQ=4,代入函数解析式可得yQ=5,当然用yE yB=yP yQ可求得点P的纵坐标,由于本题只求点Q的坐标,求点P的坐标不再叙述(下同).
②当EP做对角线时,可得,xE xP=xB xQ,即1 2=5 xQ,得xQ=一2,代入函数解析式得yQ=一7.
③当EQ做对角线时,可得xE xQ=xB xP,即1 xQ=5 2,得xQ=6,代入函数解析式得yQ=一7.
综上所述,点Q的坐标为(一2,一7)或(6,一7)或(4,5).
以上就是对于平行四边形存在性问题的解法,同学们看后自己体会每种方法的优缺点,具体到不同的题目,灵活运用某一种方法,力求简捷明快,得心应手。
感谢大家的关注、转发、点赞、交流!
,




