我们学到的均值不等式一般指x^2 y^2>=2xy。这个不等式是非常好推导的。它利用了平方数的非负性。

由(x-y)^2>=0,左边展开就可以得到x^2-2xy y^2>=0,移项就可以得到x^2 y^2>=2xy,当且仅当x=y时, x^2 y^2=2xy。然而,真正的均值不等式,其实远没有这么简单。我们所学的只是均值不等式中的一部分,而且是这个部分中的特例。
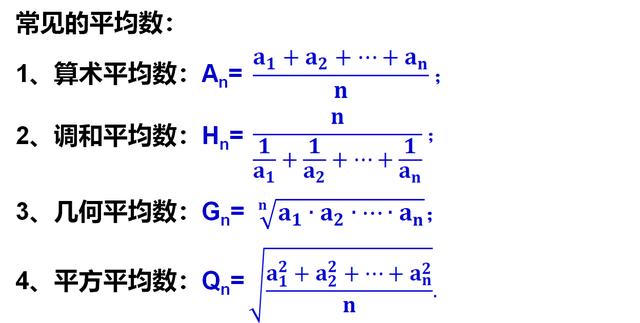
真正的均值不等式指的是调和平均数不大于几何平均数,几何平均数又不大于算术平均数,算术平均数不大于平方平均数。这里有四个平均数,都可称为均值,它们分别调和平均数,一般记做Hn,几何平均数一般记做Gn,算术平均数一般记做An,平方平均数一般记做Qn。即完整的均值不等式应该是指Hn<=Gn<=An<=Qn。

这几个平均数到底指的是什么呢?数术平均数大家应该都很清楚了,就是一组数的和除以这组数的个数;几何平均数知道的人应该也不少,就是一组数的积开n次方,n就是这组数的个数;调和平均数则是一组数的倒数的算术平均数的倒数,晕不晕?好好理解一下。平方平均数则是一组数的各个数平方的算术平均数的算术平方根。
我们一般说的均值不等式,就是Gn<=An在两个数之间的平均数关系。然而真正的均值不等式,是可以涉及到更多个数,甚至是无穷个数的。
这两个数就是x^2和y^2,而它们的算术平均数就是(x^2 y^2)/2,它们的几何平均数则是根号内(x^2y^2)=xy. 注意了,这里要求x和y同号,甚至我们通常会要求x和y都是正数。而前面的推导过程中,却是允许x和y异号的,因为当x和y异号时,x^2 y^2>0,2xy<0,自然就有x^2 y^2>2xy成立。但这里要使根号内(x^2y^2)=xy成立,就必须要求x和y同号,甚至都为正数。
根据几何平均数不大于算术平均数,就有xy<=(x^2 y^2)/2,两边同时乘以2,就可以得到x^2 y^2>=2xy。大家应该发现了,我们这里所取的两个数是x^2和y^2,为什么要取平方呢?其实这真的是没有必要的。我们也可以取两个正数x和y,然后根据几何平均数不大于算术平均数,就有根号(xy)<=(x y)/2,两边同时乘以2,就可以得到“均值不等式”的另一个形式:x y>=2倍根号(xy)。

如果把“几何平均数不大于算术平均数”当做鸡的话,那么x^2 y^2>=2xy和x y>=2倍根号(xy)都是它的蛋。问题来了,究竟是先有鸡还是先有蛋呢?事实上,Gn<=An本身就是由一个数和两个数的特殊情况,运用数学归纳法的思想推广到更多个数,甚至是无穷个数的情况的。

所以是由两个数的均值不等式,推导出完整的均值不等式,而两个数的均值不等式,又是完整的均值不等式的一个部分。老黄可不是想把你绕糊涂。老黄想说的是,由差的完全平方不小于0,展开得到两个数的均值不等式很简单,但我们不能满足于这种程度,而应该继续深扒背后的更深层次的知识。至于如何用数学归纳法的思想证明完整的均值不等式,包括调和不等式和平方不等式的关系等,不是这里要讲的重点,有机会老黄再继续和大家分享!
,




