MC物理 我为满分而来
在力学压强板块,柱体切割的题型千变万化,下面这道题我认为可以作为一道基础原型题,值得我们认真学习思考。
【题干】
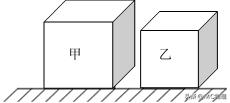
如图所示,甲、乙两个实心均匀正方体分别放在水平地面上,它们对水平地面的压强相等。则甲、乙密度ρ甲 ① ρ乙,若在两个正方体的上部沿水平方向分别截去相同高度的部分。
截去部分的质量△m甲 ② △m乙;
正方体对水平地面压力的变化量△F甲 ③ △F乙;
正方体对水平地面压强的变化量△p甲 ④ △p乙。
剩余部分的质量m’甲 ⑤ m’乙;
剩余部分对水平地面的压力F’甲 ⑥ F’乙;
剩余部分对水平地面的压强p’甲 ⑦ p’乙 。
(在上面的空格中选填:“ > ”、“ < ”、或“ = ”)
【分析】
题干信息:边长不同的两个实心均匀正方体、初始压强相等、水平方向切割相同高度△h。
设问信息:
物体密度:ρ
变化量:质量△m 压力△F 压强△p
末态:质量m’ 压力F’ 压强p’
公式选择:
由于是放置在水平地面上的密度均匀、质量分布均匀的柱形固体,因此会用到两个压强公式:
p=F/s p=ρgh
又因为涉及到水平切割,故而会用到压强的推导式:
△p = ρg△h △p=△F/s p末=p初-△p
结合题设还可能会用到的基本公式是:
F=G=mg=ρVg=ρShg
【解析·注意我们求解的顺序】
①根据初始压强相等,即p甲 = p乙,ρ甲gh甲=ρ乙gh乙,其中h为两个正方体的边长,因为h甲 > h乙,所以ρ甲 < ρ乙。
④根据切割的高度△h相同,根据公式△p =ρg△h和①可知:
△p甲=ρ甲g△h < ρ乙g△h=△p乙
⑦初始压强相等,且根据公式:p末 = p初-△p和④可知:p’甲 > p’乙
⑥根据p=F/S可以得到:F’甲=p’甲S甲 > p’乙S乙=F’乙
⑤根据F=G=mg,可以得到:m’甲=F’甲/g m’乙=F’乙/g
所以m’甲>m’乙

那么现在第②和第③问应该如何求解呢?

我们介绍一种思路:

我们向右翻转这两个正方体:

翻转成这个样子(虚线仍是原初切割线):

因为甲和乙是正方体,所以翻转之后,甲乙对地面的压强仍然和翻转前一样,且仍有p甲 = p乙。那么对于右侧被截去的部分,我们可以计算出其在上图中对地面的压力。显然,甲被截去部分此时和地面的接触面积要大于乙被截去的那部分。因此,根据F=pS,可以很轻松的求得:
△F甲=△G甲 > △G乙= △F乙
再由△G = △mg
可求得:△m甲 > △m乙
综上可解,建议收藏学习,也欢迎留言交流。