一、二次根式的概念及性质:
① 二次根式的概念:
一般地,形如 √a (a≥0)的式子叫作二次根式,其中“ √ ” 称为二次根号,a 称为被开方数。
例如,√2 ,√(x^2 1) ,√(x-1) (x≥1) 等都是二次根式 。
② 二次根式的性质:
当 a ≥ 0 时,√a 表示 a 的算术平方根,所以√a 是非负数 ( √a ≥ 0),即对于式子 √a 来说,不但 a ≥ 0,而且 √a ≥ 0,因此可以说 √a 具有双重非负性 。
③ 最简二次根式:
1、被开方数中不含有分母 ;2、被开方数中不含有能开得尽方的因数和因式 。
④ 积的算术平方根的性质:
积的算术平方根,等于积中各因式的算术平方根的积。

⑤ 商的算术平方根的性质:
商的算术平方根,等于被除式的算术平方根除以除式的算术平方根。
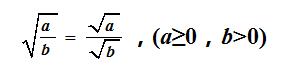
注:对于商的算术平方根,最后结果一定要进行分母有理化。
⑥ 分母有理化:
化去分母中根号的变形叫作分母有理化,分母有理化的方法是根据分数的基本性质,将分子和分母分别乘分母的有理化因式(两个含有二次根式的代数式相乘,如果它们的积不含二次根式,就说这两个代数式互为有理化因式)化去分母中的根号。
⑦ 化成最简二次根式的一般方法:
1、将被开方数中能开得尽方的因数或因式进行开方;
2、若被开方数含分母,先根据商的算术平方根的性质对二次根式进行变形,再根据分母有理化的方法化简二次根式;
3、若分母中含二次根式,根据分母有理化的方法化简二次根式 。
判断一个二次根式是否为最简二次根式,要紧扣最简二次根式的特点:
(1)被开方数中不含分母;
(2)被开方数中不含能开得尽方的因数或因式;
(3)若被开方数是和(或差)的形式,则先把被开方数写成积的形式,再判断,若无法写成积(或一个数)的形式,则为最简二次根式 。
⑧ 二次根式的加减:
(1)先把每个二次根式都化成最简二次根式;
(2)把被开方数相同的二次根式合并,注意合并时只把“系数”相加减,根号部分不动,不是同类二次根式的不能合并,即

二、知识点讲解:
1、二次根式的概念及有意义的条件:
例题1、下列式子中,是二次根式的有 ( B )

例题2、使式子 √(m-2) 有意义的最小整数 m 的值是 2 。
2、最简二次根式:
例题3、√32 不是(填“是”或“不是”)最简二次根式,若不是它可以化简为 4√2 。
3、积或商的算术平方根:
例题4、化简下列各式:


4、二次根式的运算:
例题5、计算下列各式:

三、知识拓展与提高:
例题6、

参考答案:

例题7、阅读下列材料:

将分母中的根号去掉,这种方法叫做分母有理化。
请化简下列式子:

参考答案:

例题8、观察下列各式及验证过程


请验证下列式子:

参考答案:


欢迎关注“尚老师数学”!
,




