函数的极值与最值包含的内容还是比较丰富的,涉及的问题也比较多,解决问题的思路比较广、方法也比较灵活,解题要遵循数学自身内在的逻辑规律,寻求通性通法,以不变应万变。比如分类讨论的思想、等价转化的思想、等量代换的思想、模型化的思想等等。

经典例题:
已知函数f(x)=(2 x ax^2)ln(1 x)-2x.若x=0是f(x)的极大值点,求a.
思路分析:本题的常规思路是对参数a进行分类讨论,结合f(x)的单调性,并根据极大值的定义进行分别求解。当然,简捷的途径是直接根据导数极值的定义直接进行求解。
解析:
由题意知f(x)=(2 x ax2)ln(1 x)-2x,则

且f′(0)=0。
若x=0是f(x)的极大值点,则f′(x)在x=0附近单调递减。
设h(x)=f′(x),则
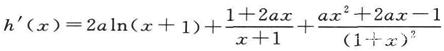
且h′(0)=0,
若f′(X)在X=0附近单调递减,则h′(x)≤0在x=0附近成立,且h′(x)在x=0处取得极大值0。
设m(x)=h′(x),则

所以m′(0)=6a 1=0,解得a=-1/6。
因此,若x=0是f(x)的极大值点,则a=-1/6。

构建模板:利用导数研究函数的极值、最值问题主要是通过计算函数的导函数,进而求解关于导函数的不等式,从而确定函数的单调性,据此分析求得函数的极值与最值.破解此类题的关键点如下.
①分析函数的单调性.结合题意,先求导函数,再确定何时f′(x)>0,何时f′(x)<0,据此可得函数的单调性.
②确定函数的极值、最值.以所得函数的单调性为切入点,可以画出函数的大致图象,以便迅速确定函数的极值情况(若在某点处左增右减,则函数有极大值;若在某点处左减右增.则函数有极小值)及最值情况(函数图象上的最高点的纵坐标为最大值.最低点的纵坐标为最小值),真正体现“数形结合”的灵活运用.
,