阻抗,以欧姆为单位,是指对包含电阻和电抗的交流电路电流的有效电阻。

我们在前面的教程中已经看到,在包含正弦波形的交流电路中,电压和电流相量以及复数可以用来表示复数。
我们在前面的正弦函数中也看到了时域转换可以转换为空间或相量域因此,可以构造相量图来找到这个相量-电压-电流关系。
既然我们知道了如何将电压或电流表示为相量,我们可以在应用于基本无源电路元件(如交流电阻当连接到单相交流电源时。
任何理想的基本电路元件,如电阻,都可以用数学的方式描述其电压和电流电阻器,我们看到,通过纯欧姆电阻器的电压与流过它的电流成线性比例,正如欧姆定律所定义的那样。考虑下面的电路。
正弦电源交流电阻

当开关闭合时,交流电压,五将应用于电阻器,R. 此电压将导致电流流动,而电流又会随着施加电压的正弦上升和下降而上升和下降。由于负载是一个电阻,电流和电压都将达到其最大值或峰值,并在完全相同的时间下降到零,即它们同时上升和下降,因此称为鈥同相 ”.
然后流过交流电阻的电流随时间呈正弦变化,用表达式表示,I(t) = Im x sin(ωt θ),其中伊姆河是电流的最大振幅 d是它的相角。另外,我们也可以说,对于任何给定的电流,我流过电阻器的最大或峰值电压R由欧姆定律得出:

电流的瞬时值,我将:

因此,对于纯电阻电路,流过电阻器的交流电流与施加在电阻上的电压成比例地变化,遵循同样的正弦曲线。由于电压和电流的供电频率相同,其相量也将相同,从而导致电流与电压“同相”(θ = 0 ).
换句话说,当使用交流电阻时,电流和电压之间没有相位差,因为只要电压达到其最大值、最小值和零值,电流就会达到最大值、最小值和零值,如下所示。
交流电阻的正弦波形

这种鈥渋n相鈥效应也可用相量图表示。在复域中,电阻是一个实数,这意味着没有鈥j或者想象中的分量。因此,由于电压和电流都是同相的,所以不会有相位差(θ = 0)在它们之间,所以每一个量的向量都是沿着同一个参考轴相互作用的。从正弦时域到相量域的变换如下。
交流电阻相量图

相量表示电压和电流量的均方根值,而不像矢量表示峰值或最大值,将上述时域表达式的峰值除以 He two相应的电压电流相量关系如下所示。
RMS关系


这表明交流电路中的纯电阻产生电压和电流相量之间的关系,其方式与直流电路中相同电阻的电压和电流关系完全相同。然而,在直流电路中,这种关系通常被称为抵抗,由欧姆定律定义,但在正弦交流电路中,这种电压-电流关系现在称为阻抗. 换句话说,在交流电路中,电阻叫做“阻抗”。
在这两种情况下,这种电压电流(V-I型)在纯电阻中,关系总是线性的。所以当在交流电路中使用电阻时阻抗,符号Zis the generally used to mean its resistance. Therefore, we can correctly say that for a resistor, DC resistance = AC impedance , orR = Z .
阻抗矢量用字母表示(Z)对于以欧姆为单位的交流电阻值( 哦)与直流电相同。阻抗(或交流电阻)可定义为:
交流阻抗
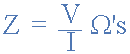
阻抗也可以用复数表示,因为它取决于电路的频率, o当存在反应性成分时。但在纯电阻电路的情况下,该无功分量将始终为零,并且在以复数形式给出的纯电阻电路中,阻抗的一般表达式为:
Z = R j0 = R Ω’s
由于纯电阻交流电路中电压和电流之间的相位角为零,因此功率因数也必须为零,并给出如下公式:成本0o= 1.0,则电阻器中消耗的瞬时功率由下式得出:

然而,由于电阻或无功电路中的平均功率取决于相角,而在纯电阻电路中,这等于θ = 0,功率因数等于1,因此交流电阻消耗的平均功率可通过使用欧姆定律简单地定义为:

与直流电路相同的欧姆定律方程。那么交流电阻消耗的有效功率等于直流电路中同一电阻消耗的功率。
许多交流电路,如加热元件和灯,仅由纯欧姆电阻组成,并且包含阻抗的电感或电容值可以忽略不计。
在这样的电路中,我们可以两者兼用欧姆定律 ,基尔霍夫定律以及简单的电路规则,用于计算和计算直流电路分析中的电压、电流、阻抗和功率。使用这些规则时,通常只使用RMS值。
交流电阻示例1交流电阻为60欧姆的电热元件连接在240V交流单相电源上。计算从电源引出的电流和加热元件消耗的功率。同时绘制相应的相量图,显示电流和电压之间的相位关系。
1电源电流:

2交流电阻消耗的有功功率计算如下:

三。由于电阻元件中没有相位差(θ = 0),相应的相量图如下:

正弦电压供应定义为:V(t) = 100 x cos(ωt 30o )与50欧姆的纯电阻相连。确定其阻抗和流过电路的电流峰值。绘制相应的相量图。
电阻上的正弦电压与纯电阻电路中的电源电压相同。将此电压从时域表达式转换为相量域表达式可以得到:

应用欧姆定律可以得到:

相应的相量图应为:

在纯欧姆电路中交流电阻电流和电压都是“同相”的,因为它们之间没有相位差。流过电阻的电流与通过电阻的电压成正比,在交流电路中这种线性关系被称为阻抗 .
阻抗,用字母表示Z,在纯欧姆电阻中,是一个复数,仅由实际交流电阻值的实部组成(R)零虚部(j0公司). 因此,欧姆定律可用于含有交流电阻的电路中,以计算这些电压和电流。
在下一个关于交流电感的教程中,我们将研究一个电感的电压-电流关系,当一个稳态正弦交流波形被应用到它,以及它的相量图表示纯和非纯电感。
,




