美国第35届中学数学竞赛于1984年2月举行,我国有100多名高中学生应邀参加了竞赛,取得了良好成绩。这次竞赛共出了30道试题,要求90分钟内解答,平均3分钟答一道题。每题均给出了五个答案,仅有一个正确。把正确的答案指出可得5分,不答给0分,答错给-1分。
下面我们来看一道与射影定理有关的题目。
题目呈现
直角三角形ABC中,AB为斜边,AC=15,高CH分AB为AH和HB,HB=16,则△ABC的面积是
(A)120;(B)144;(C)150;(D)216;(E)144√5.
在解题之前,我们来了解一下射影定理。
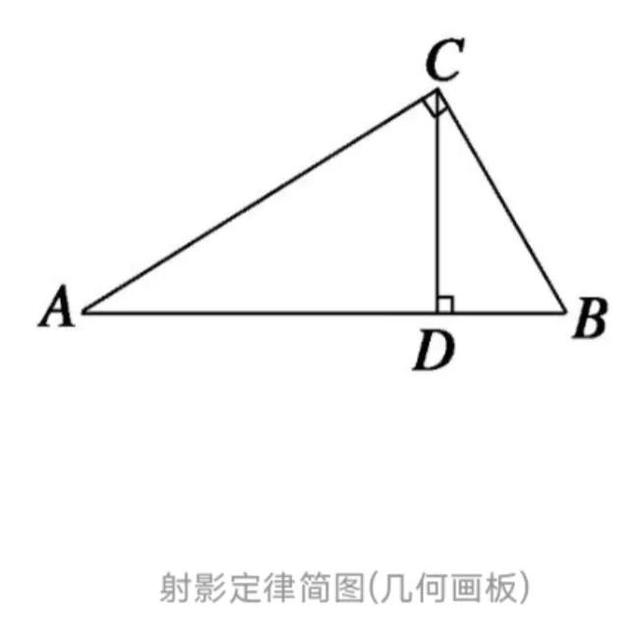
何为射影定理射影定理,又称“欧几里得定理”,定理内容是直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项,每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。公式表达为:如图,在Rt△ABC中,∠ACB=90°,cd是斜边ab上的高,则有射影定理如下:①CD²=AD·DB,
②BC²=BD·BA,
③AC²=AD·AB,
④AC·BC=AB·CD
这个射影定理从何而来?它是天上掉下来的吗?不是,它来源于欧几里得在《几何原本》中对勾股定理的证明。请看下图:

上图有三个正方形,它们称为跳舞的正方形,围成了一个直角三角形。图中还有五条辅助线,构成了欧几里得的风车。
勾股定理的证明超过400多种,欧几里得的证明独具韵味,不仅是勾股定理,还得到了射影定理。
这个图是欧几里得用来证明勾股定理的。第一条辅助线AL垂直于直角三角形的斜边,并把大正方形分为两个矩形。
欧几里得说,以BL为对角线的矩形面积等于小正方形,以CL为对角线的矩形面积等于中正方形。
因为这两个矩形面积之和等于大正方形的面积,所以,c²=a² b²,命题得证。
这两个矩形面积等于对应的正方形的面积,就是射影定理。
不明白?欧几里得继续作出AD和CF这两条辅助线,说:△ABD≌△BCF.
这个容易看出,△BCF绕B点顺时针旋转90°就与△ABD重合。
接下来进行等积变换。大家知道等积移动定理吗?保持底边,顶点在与底边平行的的直线上移动,所得的三角形面积相等。
对等积移动定理更常见的叙述是:共底边的三角形若顶点在与底边平行的直线上,则其面积相等。
这个定理的证明是轻而易举的:因为平行线间距离处处相等,所以这些三角形同底等高,从而等积。
运用等积移动定理,可得△FBA与△FBC面积相等,△BDA与△BDL面积相等。
因为△FBA面积为小正方形的一半,△BDL的面积为以BL为对角线的矩形面积的一半,所以小正方形面积等于对应的矩形面积。即AB²=射影·BC
举个例子下面我们来看一个具体的例子。

如图所示,有这样一个小学水平的题目,已知直角三角形的三边边长,求斜边BC上的高AD.
这个问题简单,利用面积关系解题:
BC·AD=AB·AC⇒
AD=AB·AC÷BC
=6×8÷10
=4.8
继续追问,BD和CD是多少?
由射影定理可得:
BD=AB²÷BC=36÷10=3.6
CD=AC²÷BC=64÷10=6.4
应用射影定理,我们可以作图作出已知线段的平方根。请看下图:

如图所示,因为CD⊥DB,AC=1,所以AD就是AB的平方根。
解答美国竞赛题有了前面的铺垫,我们来解答美国数学竞赛题。

如图所示,已知在直角三角形ABC中,AC=15,BH=16,设AH=x,据射影定理列方程:
x(x 16)=15²
x² 16x=225
用配方法解方程,
x² 16x 64=225 64
(x 8)²=289
解方程得
x₁=9,x₂=-25,
负根舍去,得AB=16 9=25,
由勾股定理可得,
BC²=625-225=400,
即BC=20,
所以三角形面积为150,答案是C。
总结看懂了欧几里得对勾股定理的证明,就容易理解记忆射影定理了。
我们可以这样记:
直角边的平方=射影·斜边
斜边上的高的平方=勾的射影·股的射影
欧几里得的证明是对简单的基础知识点的组合和综合应用,辅助线也作得漂亮。虽然看懂命题47的证明不难,当个事后诸葛亮是容易的,但是独立发现创造这个证明却是很困难的。遥想当年,欧几里得用一套组合拳完成这个令人赏心悦目的证明后,欣喜的心情必定是酣畅淋漓,值得浮一大白庆贺!
科学尚未普及,媒体还需努力。感谢阅读,再见。
,




