大家好。感谢阅读本鸡的拙作,期待你关注。
本鸡的理念是,理解数学只能类比。本文就是一个具体例子。本文专为初学微积分的选手设计,需要复习微积分概念的选手也可获益。
本文从最容易的十进制展开,一线贯通数列、级数、幂级数、函数项级数。强烈建议你读本鸡的拙作“菜鸡速通微积分:数列极限定义和极限法则,一个例子的事“。下面就是这个故事的另一个版本。
别废话,来啊。
一、从十进制展开到数列
观察下面的图,这是明摆着的,你知道的π的十进制展开:π=3.1415926...........。
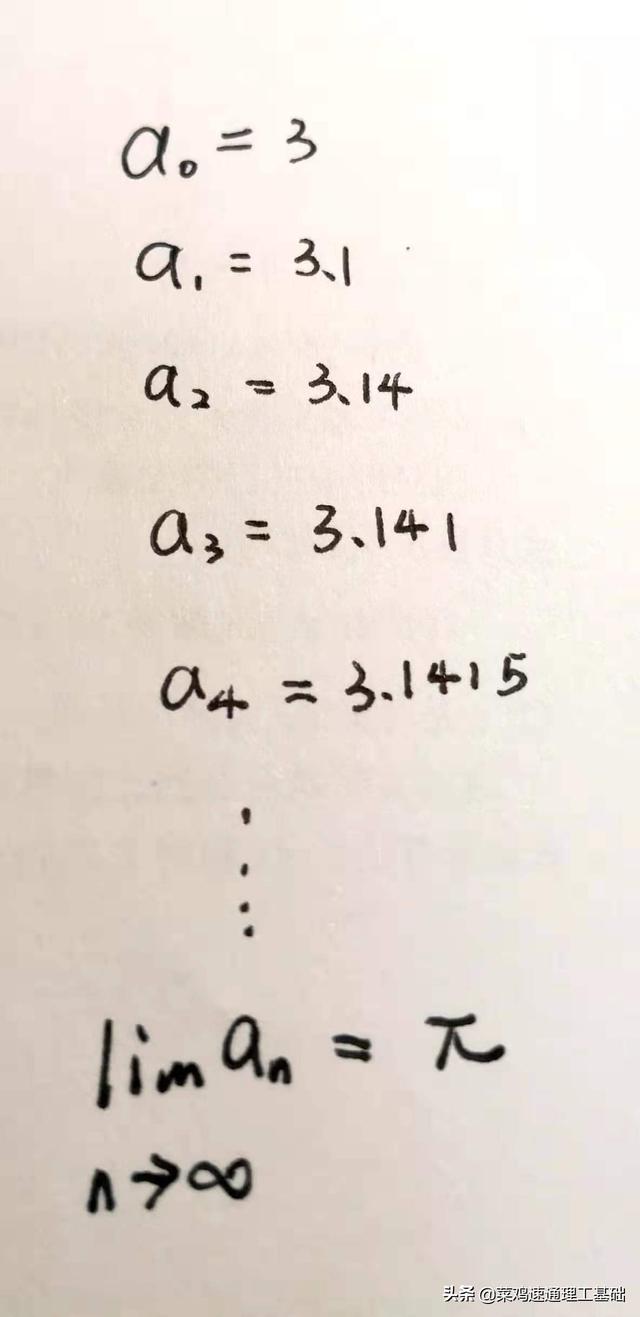
很明显,图里面写的是一个数列,并且,明摆着是一个收敛到π的数列。如果不看具体的数字,只看字母,这就是序列。请心里一直想着这个序列。有一点要强调一下,就是如果你只想用π的近似值,事实上,你永远只能用一个近似值,就可以扔掉某项以后的所有数字。比方说你写个

近似的前提是确实收敛
二、从数列到级数
现在,重要的是,这个数列可以看做一个级数(无穷和)

不论你是否写成了这个更麻烦的形式,重要的是,无穷级数的收敛性,本质上就是序列的收敛性。说得明白一点,你得明白部分和序列:只求若干有限项的和。比方说,第一张图里那些a1、a2......这个序列里面的每一个都是部分和,因此叫做部分和序列。
再麻烦些,还可以写成下面的样子,这还是废话。

位和权表达
10的负多少次方,就叫做位,其对应的乘数,就叫做权。比方说,第一位是10^0,就是个位数;个位数的值,就是权值。还是那句话,不管你怎么写,极限是π这件事是明摆着的。插一句废话,这仍然是十进制展开,重要的是任何实数都有十进制展开。
三、从级数到幂级数
稍微抽象一下,现在咱用字母代替10,比方说,你写个x=10,这样,就又变成了

如果现在x不是10,就是换不同的位,当然左边就不是π了。如果还想得到π,就必须重新写不同的权。重要的是,现在的情况更有意思了,实际上,你能想象出来,同一个数,可以写成任意进制。当然,现在的位和权必须配合好了,才能获得π。
现在咱不指定位,那么就没法指明权,写的抽象一点,就是

现在,希望你还没崩溃。当然,现在得写个更一般些的形式:

x不同,就得到不同的和
死死地盯着右边的求和号里面的东西,确保你同意,每一个都是某个幂的单项式,因此叫做幂级数。
当然,还是那句话,近似的前提是收敛。如果x可以变化,看做一个变量,那么左边就是对应的函数值了。不管怎么说,这还是个和,所以对应的和就叫和函数。
如果只写有限项,就是近似的多项式。等等!x=10收敛性是明摆着的,但是x=1呢?就变成了3 1 4 1 5 9 ........这明摆着是无穷大。一个幂级数,收敛性取决于x的值,换句话,x必须落在一范围内,才能收敛。这个范围的半径,就是收敛半径。数列审敛法,绝大多数,都能毫无困难地推广到级数理论。比如柯西准则,单调收敛,比较审敛法,更有趣的是还有积分审敛法---以后本鸡考虑推出”从十进制展开到积分“、”从十进制展开到傅里叶级数“等等系列。敬请期待。
再看看刚才的f(x)。写成刚才那个样子以后,还能进一步抽象--因为幂函数只是特殊的函数--所以,你可以看懂

特别的如果取fk(x)为三角函数,就是三角级数;取其(x-x0)的幂,就是泰勒级数,取ejwt,就是傅里叶级数...........
本文话题到此结束。
多说几句。
懂了函数项级数,就可能贯穿了实分析和复分析,概率论和泛函分析。
这里隐藏着一坨大神:拉格朗日,泰勒,洛朗,柯西,阿贝尔,斯通,维尔斯特拉斯,傅里叶,拉盖尔,贝塞尔,勒让德,勒贝格.....
不管怎么样,重要的是,这一切,都建立在序列,序列的收敛性和极限这几个根本的概念的基础上。如果谈极限存在性,就是泛函分析;如果谈极限唯一性,就是点集拓扑学;给函数项级数赋以具体的含义,就得到重心、期望、方差........
所以,极限的理论,是数学的核心理论;判断收敛的法则,是数学的核心定理。
,




