八年级上册数学第十一章《三角形》知识点总结
一、知识框架:

二、知识概念:
(一)与三角形有关的线段
1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
2.三角形按边分类
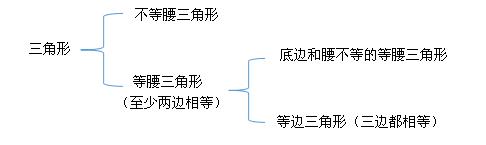
三角形的任意两边之和大于第三边。(依据是:两点之间,线段最短。)
三角形的任意两边之差小于第三边。
4.三角形的高
①AD是△ABC的高;
②AD⊥BC,垂足为D;
③D在BC上,且∠ADB=∠ADC=90°.
(3)性质特点:
①因为高是通过作垂线得出的,因而有高一定有垂直和直角.常用关系式为:
因为AD是BC边上的高,
所以∠ADB=∠ADC=90°.
②“三角形的三条高(所在直线)交于一点”
当是锐角三角形时,这点在三角形内部;
当是直角三角形时,这点在三角形直角顶点上;
当是钝角三角形时,这点在三角形外部.如图所示.

③三角形面积公式:S△ABC=1/2BC·AD
5.三角形的中线
(1)定义:三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
(2)描述方法:三角形中线的描述方法有两种方式,如图.

②间接描述:D是BC边上的中点.
(3)性质特点:
①由三角形中线定义可知,有中线就有相等的线段,如上图中,因为AD是BC边上的中线,所以BD=CD(或BD=1/2BC,DC=1/2BC).
②如下图所示,一个三角形有三条中线,每条边上各有一条,三角形的三条中线交于一点.不论是锐角三角形、直角三角形,还是钝角三角形,三角形的三条中线都交于三角形内部一点.
三角形三条中线的交点叫做三角形的重心.

③面积问题:三角形的中线平分三角形的面积(理由:等底同高)(重点)
如图,在△ABC中,AD是BC边上的中线,则S△ABD=S△ACD=1/2S△ABC.

因为BD=CD,△ABD和△ADC等底同高,所以面积相等,因此通过作三角形的中线可将三角形分成面积相等的两部分.
④周长问题:如图所示,AD是BC边上的中线,△ABD和△ACD的周长之差实质上就是AB与AC的差,这也是三角形中线中常出现的问题.

(1)定义:三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
(2)描述方法:角平分线的描述有三种,如图.

①直接描述:AD是△ABC的角平分线;
②在△ABC中,∠1=∠2,且D在BC上;
③AD平分∠BAC,交BC于点D.
(3)性质特点:
①由三角形角平分线的定义可知,有角平分线就有相等的角,如上图中,因为AD是△ABC的角平分线,所以∠1=∠2(或∠1=∠2=2(1)∠BAC,或∠BAC=2∠1=2∠2).
②一个三角形有三条角平分线,三角形的三条角平分线交于一点,不论是锐角三角形、直角三角形,还是钝角三角形,这个交点都在三角形内部.

三角形具有稳定性,四边形不具有稳定性
(二)与三角形有关的角
1.三角形的内角
①. 三角形的内角和定理
三角形的内角和为180°,与三角形的形状无关。
②. 直角三角形两个锐角的关系
直角三角形的两个锐角互余(相加为90°)。
有两个角互余的三角形是直角三角形。
2.三角形的外角
①. 三角形外角的定义
三角形的一边与另一边的延长线组成的角叫做三角形的外角。
②. 三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角之和。
三角形的一个外角大于与它不相邻的任何一个内角。
三角形外角和为360°,与三角形的形状无关。
(三)多边形
多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
多边形的内角:多边形相邻两边组成的角叫做它的内角.
多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.
多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.
与多边形有关的公式:
①从n边形的一个顶点出发可以引(n-3)条对角线;
②n边形共有n(n-3)/2条对角线;
③从n边形的一个顶点出发引出的对角线把多边形分成(n-2)个三角形;
④n边形的内角和等于(n-2)·180°;
⑤多边形的外角和为360°;






