
前些日子一道日本小升初的考试题,难住了不少同学,今天我们来分析思路。先回顾一下原题。
有一个面积为6cm²的正六边形ABCDEF。 G、H和I点在对应的FA、BC和DE边上,使得 FG: GA = BH: HC = DI: IE = 2: 1。 求彩色三角形的面积是多少cm²?
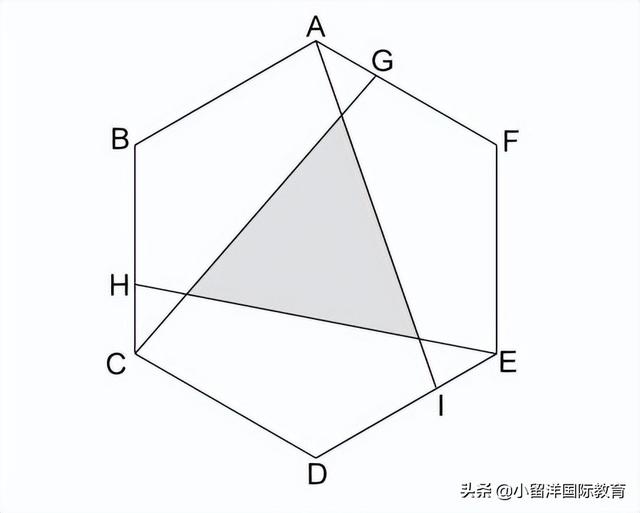
我们很多同学都在六边形内部做文章,当然也是可以的,但不是出题人的本意。还记得我们以前做过的一道题吗?把一个正三角形切成正六边形。我们这就还原回来看看。
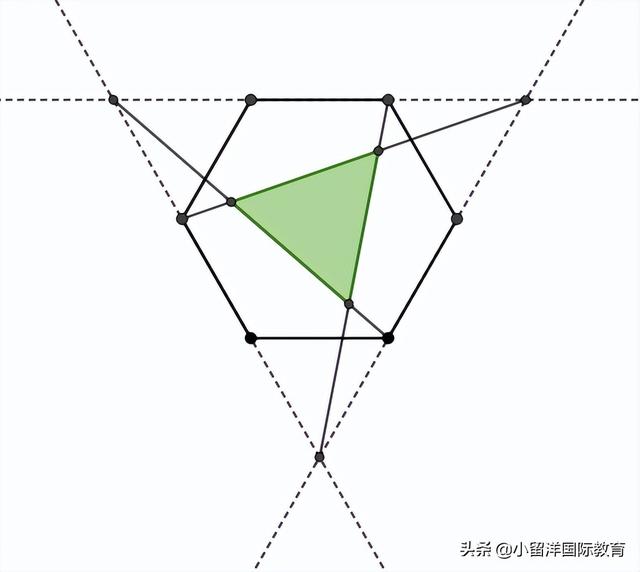
那道题出题人就是这样画的,然后抹去了作图痕迹(真够狡猾的啊)。还不相信,不确定那几条线把六角形的边切成2:1?那我们就再做条辅助线帮你观察,如下。

由相似三角形易知道,图中两个红点将正六边形的边三等分,就是2:1.
既然六边形的面积是6平方厘米,那正三角形的面积就是9平方厘米喽。经过观察得知,中间的绿色部分是由三块橙色三角形围成,如下图。


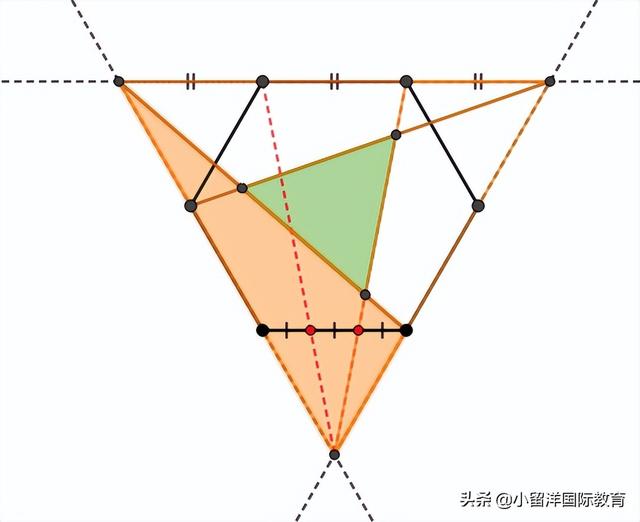
一个橙色三角形的面积也好算,底边是正三角形底边的1/3,它的面积也是1/3.,就是3平方厘米。但是要直接从大的正三角形面积中减去这三个橙色三角形的话,会有重叠部分,如下。
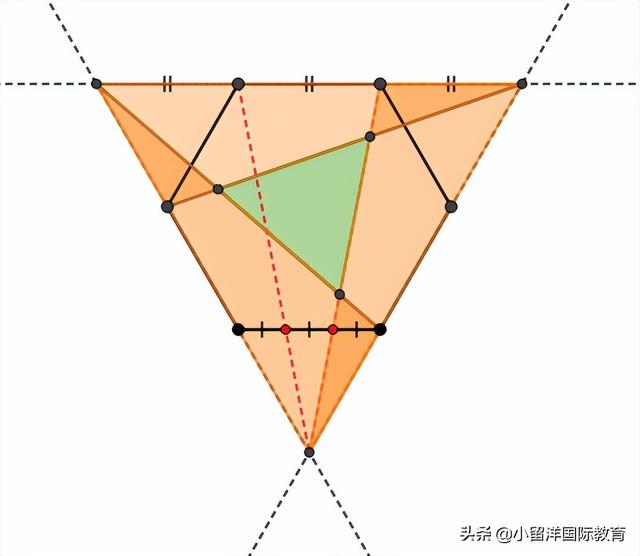
怎么算重叠部分的面积呢?我们还是观察比例关系。看下图,2个蓝色三角形,它们共享底边DH。△DIH面积好算,是2/3正三角形面积,是6平方厘米。

那△DBH的面积呢?做辅助线AD观察,原来等于△ABH的面积=1平方厘米。

△DHI和△DHB等底,面积比就是高的比,做出两个高(红线),可知是相似三角形,那么线段IK:KB=△DHI面积:△DHB面积=6:1. 往下看。

知道了IK:KB的比例,可知△KHB是△IHB面积的1/7,即3/7平方厘米。
好了回头总结下,中间绿色部分的面积=正三角形面积-3个大橙色三角形面积 3个重叠部分面积=9-3x3 3x3/7=9/7平方厘米。
当然熟练了步骤可以简化,为了让所有同学都看明白,一步一步分析而来。这道题有些技巧,就是反复应用三角形面积和边的关系。如果怕被绕晕了,也可以建立坐标系算,条条大路通罗马。
本文由小留洋Jeffrey撰写,欢迎大家分享你的思路,评论区等你们。☎ 关注「小留洋」,一起研究海外数学题。






