
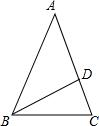
1.如图,等腰三角形ABC中,顶角∠A=36°,BD平分∠ABC,D点是AC的黄金分割点,若AC=4cm,则BD=______cm(结果保留三个有效数字)
2.在△ABC中,A1、A2、…A5为AC边上不同的点,连接BA1,图中有3个不同的三角形;再连接BA2,图中有6个不同的三角形;如此继续下去,当连接BA5时,则图中不同的三角形共有______个。

3.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An﹣1CD的平分线交于点An,设∠A=θ,则:
(1)∠A1=( );
(2)∠An=( )。

4.已知△ABC中,∠A:∠B:∠C=1:3:5,则△ABC是 ______三角形。
5.一个三角形三边长之比为2:3:4,周长为36cm,求此三角形的三边长。
6.按要求完成作图,并回答问题:如图,三角形ABC中
(1)画线段BC的中点D,并连接AD;
(2)过点A画BC的垂线,垂足为E;
(3)根据上述作图,若∠ABC=60°,则∠BAE= ______,若BD=2cm,则BC= ______cm;
(4)用“<”、“=”、“>”填空:AB AC_______BC,根据_________.

7.下面命题中:
(1)旋转不改变图形的形状和大小
(2)轴反射不改变图形的形状和大小
(3)连接两点的所有线中,线段最短
(4)三角形的内角和等于180°
属于公理的有( )
A.1个
B.2个
C.3个
D.4个
8.已知一个三角形中有两个内角之和为n°,最大角比最小角大24°,则n的取值范围是______。
9.下列四种说法:
①若一个三角形三个内角的度数比为2:3:4,则这个三角形是锐角三角形。
②“掷两枚质地均匀的正方体骰子点数之和一定大于6”是必然事件。
③购买一张可能中奖。
④已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为100°。
其中正确的序号是______
10.下列判断的语句中,错误的是( )
A.三角形三个内角的和等于180度
B.经过直线外一点有且只有一条直线垂直于已知直线
C.射线AB和射线BA表示同一条射线
D.有两个内角等于60°的三角形一定是等边三角形
//////////
不要偷看答案
//////////
==========
1.
【解析】
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
又BD平分∠ABC,
∴∠ABD=36°,
∴BD=AD,
∵D点是AC的黄金分割点,
∴BD=AD≈4×0.618≈2.47cm
【答案】2.47
2.

3.

4.
【解析】
设∠A=x,∠B=3x,∠C=5x,
∵∠A ∠B ∠C=180°,
∴x 3x 5x=180°,
解得:x=20°,
∴∠A=20°,∠B=60°,∠C=100°,
∴△ABC是钝角三角形
【答案】钝角
5.
【解析】
设三边长分别为2x,3x,4x,
由题意得,2x 3x 4x=36,
解得:x=4
【答案】
三边长为:8cm,12cm,16cm
6.
【答案】
(1)分别以B,C为圆心,
大于

BC为半径画圆,两圆相交于F,
过F作FD⊥BC于D,则点D即为BC的中点;
(2)过点A画BC的垂线,垂足为E;
(3)∵在△ABE中,∠ABC=60°,
∠AEB=90°,
∴∠BAE=180°﹣60°﹣30°=30°,
BD=2cm,则BC=2BD=4cm;
(4)AB AC>BC,根据两点之间线段最短.

7.
【解析】
(1)旋转不改变图形的形状和大小,正确且是公理;
(2)轴反射不改变图形的形状和大小,正确且是公理;
(3)连接两点的所有线中,线段最短,正确且是公理;
(4)三角形的内角和等于180°,正确但不是公理。
综上可得(1)(2)(3)正确
【答案】C
8.
【解析】
设△ABC三内角为∠A,∠B,∠A 24°,且∠A≤∠B≤∠A 24°.
当∠A=∠B时,n=∠A ∠B,可得n有最小值104°,即n≥104°.
当∠B=∠A 24°时,n=∠B (∠A 24°),可得n有最大值136°,即n≤136°
【答案】104°≤n≤136°
9.
【解析】
①若一个三角形三个内角的度数比为2:3:4,即可得出2x 3x 4x=180°,解得:x=20°,
∴三角形三个内角的度数分别为:40°,60°,80°,
∴这个三角形是锐角三角形;故此选项正确;
②“掷两枚质地均匀的正方体骰子点数之和一定大于6”是必然事件;根据掷两枚质地均匀的正方体骰子也可能出现两点数之和小于6,故此是随机事件,
故此选项错误;
③购买一张可能中奖;是随机事件,故此选项正确;
④已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为100°,此三角形顶角也可能是40°,故此选项错误。
【答案】①③
10.
【解析】
A、符合三角形的内角和定理,故本选项正确,不符合题意;
B、是垂线的性质,故本选项正确,不符合题意;
C、射线AB和射线BA的端点不同,延伸方向不同,故本选项错误,符合题意;
D、符合等边三角形的判定,故本选项正确,不符合题意。
【答案】C
,




