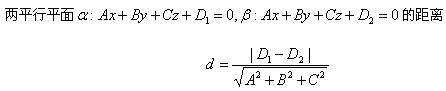既然扯开了向量,扯开了坐标系,不继续深挖有点过不了自己的关。
从平面直角坐标系类比过来,取空间一点O建立空间直角坐标系,在空间直角坐标系中,一个曲线或者曲面显然也可以象平面直角坐标系那样,用方程或者方程组来表示。我们将分几期来介绍几个常见的几何体。今天先说说最简单的——平面。

很容易理解的一个结论,不过似乎不太容易记。我们可以这样改造一下。
令

则平面方程可以写成

这就是平面的一般方程。前面的方程也可以称为点法式方程。
举个例子。
如果平面过三点

,求平面ABC的方程
解:设平面方程为

则

平面的方程为

其中,a,b,c是平面在三个坐标轴上的截距。
哇塞,这个方程似乎很好记,很优美漂亮。我们也给它一个名字,叫做截距式。(因为这个方程和直线的截距式长得太像了,对吧)
数学不做题,犹如游泳不下水。还是来几个题玩一下。
例1、求过点

的平面方程。
解:设平面方程为

则

从方程可以直接看出,平面的法向量为(14,9,-1)
例2、已知平面过原点及点(6,-3,2),且与平面4x-y 2z=8垂直。求平面的方程

显然,对于两个平面

则

让我们继续大胆猜一猜。