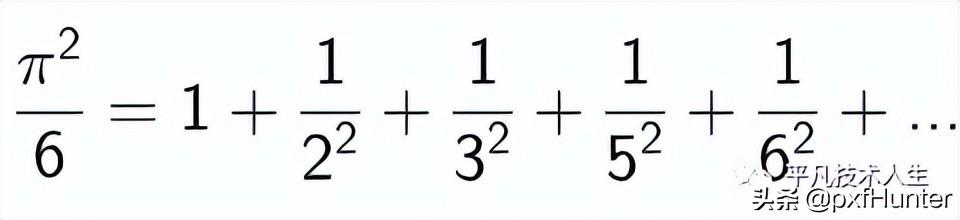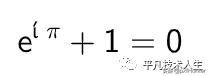“ 父母对孩子的爱,就像圆周率π,无限不循环。”

之前用scratch工具,通过圆内切正多边形的方式,自行计算过π的实验数值是:3.14185107。
通过上面的公式继续计算可得:π=3.14185107。
京京爸,公众号:平凡技术人生和京京一起探索π的秘密
之前说了我国古代人们对π的认知过程。其实在差不多同一时间线上,国外也有人发现π的秘密。比如,π在国外也被称为“阿基米德数”。就是由于古希腊的大数学家、物理学家阿基米德做试验得出π=3.14的。
阿基米德用的方法和我们上次方法一致。也是内切正多边形方法,当他内切正多边形到正96边形的时候,算出π的值大约是3.14。公式如下:
随着人类的发展,时间的推移,到了约1500年左右,印度的一名数学大师发现了关于π的一个优美的公式。
这个公式,很容易的可以简化成下面的公式:
这个公式据说最早是印度数学家发现的。但其实,能追溯到记录的是欧洲数学家发现的。公式现如今被称为:格里高利-莱布尼茨公式。这个公式用简单分数无穷加和的方式来计算π值。
之所以能用这种方法,得益于当时微积分的发明。微积分让这类无穷累加的运算变得更加容易。而微积分方程也是莱布尼茨和牛顿先后独立发现的。
而大数学家欧拉,莱昂哈德.欧拉在1734年证明了另一个优美的公式:
仔细观察这个公式,能发现一个公式中,竟然同时汇聚包含了3条浩瀚的数学支流。几何(数字π),算术(奇数序列与平方序列)和无穷分析(无穷加和)。能看出来π不单单是一个几何概念。
π的另一层含义是:它是一个无理数(无理数,也称为无限不循环小数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。)。
欧拉还有另一个关于π的最美方程式,初始方程式为:
当,x=π时候,cos(π)=-1,sin(π)=0,上面方程变化为:
这个公式就更加的厉害了。它非常牛逼的将 e,i,π,1,0 5个微妙且看似无关的数学符号紧密地联系在一起,其美妙之处让人称绝。大数学家高斯,看到这个公式都连连称奇,赞不绝口。
正是由于π的无限不循环,在人们每次提升认识π小数点后面的位数的同时,又会发现π的其他不为人知的秘密。目前看来,人们离非常清晰的认识π还有一定的距离。
,