利用导数证明不等式
函数如果连续可导,利用导数为零的点及函数的单调性,就可以证明某些不等式。
首先复习一下预备知识。
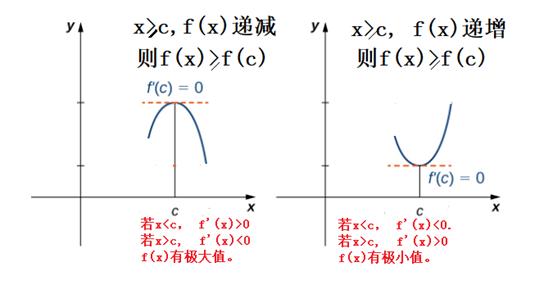
如果f(x)在c处有一个局部极值并且f(x)在c处是可导的,那么f ' (c) = 0, 反之亦然。
若f(c) 是极大值,则有f(x)<f(c); 若 f(c) 是极小值,则有f(x)>f(c)。
示例1:若x>0, 证明ln(x)≦x-1 .
证: 令f(x)=ln(x)-(x-1)
则f’(x)=1/x-1, 当f’(x)=0, 则x=1,
当0<x<1时, f’(x)>0,
当x>1时, f’(x)<0,
因此x=1, 函数 f(x)有最大值f(1)=0,
所以f(x) =ln(x)-(x-1) ≦0, 就是ln(x)≦x-1, 证毕。
示例2:若x>0, 证明1 2lnx≦x2
证:令f(x)=-( 1 2lnx)
则f’(x)= 2x-2/x-=2(-1)/x , 当f’(x)=0, x=1 (x=-1舍去)
当0<x<1时, f’(x)<0,
当x>1时, f’(x)>0,
因此x=1, 函数 f(x)=-( 1 2lnx)有最小值f(1)=0,
所以f(x) = -( 1 2lnx)≥0, 就是 ( 1 2lnx) ≦ ,证毕。






