找出数列的排列规律(二)
这一讲我们利用前面学习的等差数列有关知识和找规律的思想方法,解决数学问题
(一)例题指导例1. 如果按一定规律排出的加法算式是3 4,5 9,7 14,9 19,11 24,……,那么第10个算式是( ) ( );第80个算式中两个数的和是多少?
分析与解:
第一个加数如下排列:3,5,7,9,11……,这是一个等差数列,公差是2,第二个加数排列如下:4,9,14,19,24,……,这也是一个等差数列,公差是5。
根据等差数列的通项公式可以分别求出第10个算式的两个加数。
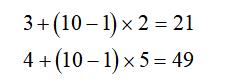
所以第10个算式是21 49。
要求第80个算式的和,只要求出第80个算式的两个加数,再相加即可,当然也可以找一找和的规律。
想一想:第几个加法算式中两个数的和是707?
例2. 有一列数:1,2,3,5,8,13,……,这列数中的第200个数是奇数还是偶数?
分析与解:要想判断这列数中第200个数是奇还是偶,必须找出这列数中奇、偶数的排列规律。
不难看出,这列数是按照“奇偶奇”的顺序循环重复排列的,即每过3个数循环一次。那么到第200个数一次循环了66次还余2。这说明到第200个数时,已做了66次“奇偶奇”的循环,还余下2个数。也就是说余下的两个数依次为“奇偶”,所以第200个数是偶数。
例3. 下面的算式是按某种规律排列的:1 1,2 3,3 5,4 7,1 9,2 11,3 13,4 15,1 17,……
问:(1)第1998个算式是( ) ( );
(2)第( )个算式的和是2000。
分析与解:
(1)第1个加数依次为1、2、3、4,1、2、3、4……每4个数循环一次,重复出现。1998÷4=499·······2,所以第1998个算式的第1个加数是2。第二个加数依次为1,3,5,7,9,11……是公差为2的等差数列。根据等差数列的通项公式可求出第1998个算式的第2个加数为1 (1998-1)x2=3995,所以第1998个算式是2 3995。
(2)由于每个算式的第二个加数都是奇数,所以和是2000的算式的第1个加数一定是奇数,不会是2和4。只有1 x=2000或3 x=2000。其中x是1、3、5、7、9……中的某个数。
若1 x=2000,则x=1999。根据等差数列的项数公式得:(1999-1)÷2 1=1000,这说明1999是数列1、3、5、7、9……中的第1000个数,因为1000÷4=250,说明第1000个算式的第1个加数是4,与假设1 x=2000矛盾,所以x≠1999;
若3 x=2000,则x=1997。与上同理,(1997-1)÷2 1=999,说明1997是等差数列1、3、5、7、9……中的第999个数,由于999÷4=249···3,说明第999个算式的第一个加数是3,所以,第999个算式为3 1997=2000。
例4. 将1到200的自然数,分成A、B、C三组:
A组:1 6 7 12 13 18……
B组:2 5 8 11 14 17……
C组:3 4 9 10 15 16……
根据分组的规律,请回答:
(1)B组中一共有( )个自然数;
(2)A组中第24个数是( );
(3)178是( )组里的第( )个数。
分析与解:(1)B组中的数成等差数列,其首项是2,公差是3,从整个数表看,竖着数是每3个数一组,因为200÷3=66····2,所以200是B组中的最后一个数,根据等差数列的项数公式。(200-2)÷3 1=67。所以,B组中一共有67个自然数。
(2)观察A组中数的排列规律,由于24是偶数,所以应特别注意偶数位置上的数的排列规律。第几个数就是3的几倍,第24个数就是3的24倍,所以A组第24个数是。
(3)观察A、B、C三组数(竖看),每2列为一组(6个数),……4,说明重复29次,还剩下4个数,这4个数重新排列一下可知,178排在C组。每一组含有C组的2个数。最后余下的4个数,在C组又排了2个,所以178在C组中是第个数。
[答题时间:40分钟]
(二)尝试体验1. 如下图所示,黑珠、白珠共102个,穿成一串,这串珠子中,最后一个珠子是( )颜色的,这种颜色的珠子共有( )个。
○●○○○●○○○●○○○……
2. 有红、白、黑三种纸牌共158张,按5张红色,后3张白色,再4张黑色的次序排列下去,最后一张是( )色,第140张是( )色。
3. 节日的校园内挂起了一盏盏小电灯,小明看出每两个白灯之间有红、黄、绿各一盏彩灯,小明想,第73盏一定是( )色灯。
4. 下面的算式是按一定的规律排列的:4 2,5 8,6 14,7 20……,那么,第100个算式的得数是( )。
5. 找规律,按规律填数。
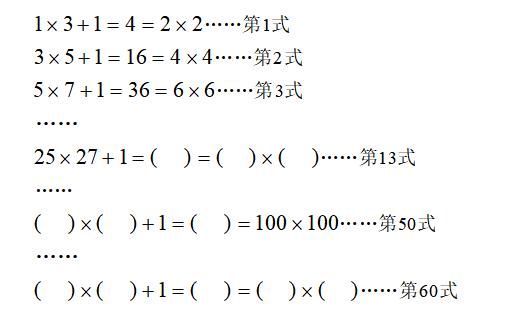
6. 自然数按一定规律排成下表形式,问:第10行第5个数是多少?

【试题答案】
1. 如下图所示,黑珠、白珠共102个,穿成一串,这串珠子中,最后一个珠子是( )颜色的,这种颜色的珠子共有( )个。
○●○○○●○○○●○○○……
除去第一个珠子,剩下的(102-1=)101颗珠子是按照“一黑三白”的次序循环重复的。
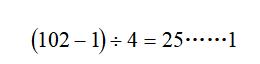
说明循环了25次后还多出一个黑珠子,所以最后一个珠子是黑色的,黑色的珠子共有26个。
2. 有红、白、黑三种纸牌共158张,按5张红色,后3张白色,再4张黑色的次序排列下去,最后一张是( )色,第140张是( )色。
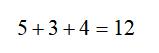
这是按“5红3白4黑”循环排列的,它的循环周期是12。
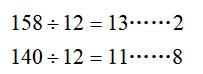
所以最后一张是红色,第140张是白色。
3. 节日的校园内挂起了一盏盏小电灯,小明看出每两个白灯之间有红、黄、绿各一盏彩灯,小明想,第73盏一定是( )色灯。
把排列的顺序写出来是:白、红、黄、绿、白、红、黄、绿、白、红、……是按“白、红、黄、绿”循环排列的。
所以第73盏灯一定是白色的。
4. 下面的算式是按一定的规律排列的:4 2,5 8,6 14,7 20……,那么,第100个算式的得数是( )。
第一个加数这样排列:4,5,6,7,……(公差是1的等差数列)
第二个加数这样排列:2,8,14,20,……(公差是6的等差数列)
根据等差数列的通项公式得:
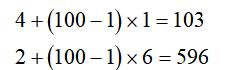
所以,第100个算式的得数是103 596=699
5. 找规律,按规律填数。
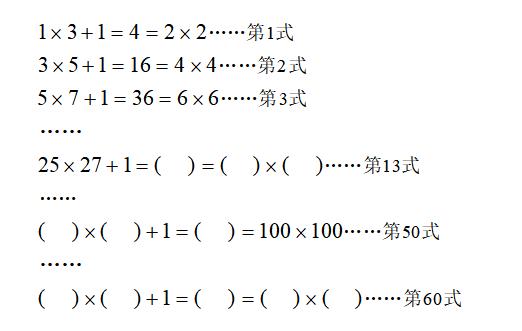
第一个等号前的两个因数是两个相邻的奇数,第二个等号后面的因数介于前面两个奇数之间。如第3式:5和7之间只有一个自然数(6)。除此之外,第一个等式的第一个因数是一个公差为2的等差数列(1,3,5,7……)
根据以上规律可得:
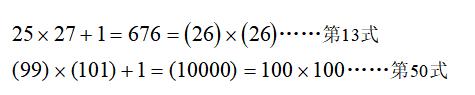
第60式中未知数较多,只要求出第一个等号前的第一个因数就好填了。
根据等差数列的通项公式可得:1 (60-1)×2=119
所以第60式为:(119)×(121) 1=(14400)=(120)×(120)
6. 自然数按一定规律排成下表形式,问:第10行第5个数是多少?

第一行1个数,第二行2个数,第3行有3个数……,第几行就有几个数,我们先求出到第九行结束一共有多少个数,然后再继续数出5个就可以了。
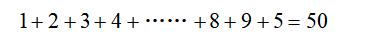
所以,第10行的第5个数是50。
坚持每天与大家分享小学数学提高课程,希望爸爸妈妈点赞转发收藏给自己的孩子学习~如果有什么不懂的问题,私我,有时间给你们解释不懂的问题!
点赞转发收藏评论是我的动力!
,




