|作者:崔廉相 许康 张芃 孙昌璞
(1 北京计算科学研究中心)
(2 中国工程物理研究院研究生院)
(3 中国人民大学物理学系)
本文选自《物理》2023年第1期

摘要 2022年诺贝尔物理学奖授予法国、美国和奥地利的三位科学家阿兰·阿斯佩、约翰·弗朗西斯·克劳泽和安东·塞林格,以表彰他们利用纠缠光子实验检验贝尔不等式以及在开拓量子信息科学方面做出的卓越贡献。贝尔不等式在量子力学基本问题和量子信息研究中都有着不可或缺的地位,它的违背直接揭示了量子力学的基本特征——量子非定域性。文章在讲清楚基本科学概念的基础上,简要介绍了贝尔不等式理论的建立及验证其违背的实验研究的科学历程。为了解决EPR佯谬,基于玻姆的定域隐变量理论,约翰⋅贝尔提出了关于纠缠态上的关联测量满足的基本不等式——贝尔不等式。他还发现,量子力学关于关联的计算结果违背贝尔不等式,可以在类空距离上展现出“鬼魅”的长程量子关联。这种长程关联看似有超光速的“超距作用”,但这只是人们明显或潜在地使用了“波包塌缩假设”。EPR文章明显地采用这个假设推断远方客体共存的物理实在要素,由此对量子力学完备性提出质疑。文章评述了阿斯佩、克劳泽和塞林格荣获诺贝尔物理学奖的关于贝尔不等式违背的判定性实验,介绍了华人物理学家在纠缠态和贝尔不等式研究方面的基础性贡献,包括早年吴健雄利用正负电子湮灭产生EPR光子的先驱性实验,李政道和杨振宁关于产生两个中性K介子
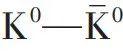
关键词 2022年诺贝尔物理学奖,贝尔不等式,EPR佯谬,量子纠缠
引 言
量子力学的建立不仅奠定了当代物质科学的理论基础,而且在应用方面也取得了巨大的成功,推动了当代的技术革命。然而,自量子力学诞生起,对于量子力学诠释(interpretation of quantum mechanics)——波函数如何刻画微观世界这一问题,长时间以来人们并未达成共识。玻恩几率解释是量子力学哥本哈根诠释的核心。它认为,对于处在特定量子态的系统,在对某个力学量进行测量之前,量子力学并不能确定性地预言测量结果,只能给出各种可能结果出现的概率。这种概率性的预言需要通过对大量处于相同量子态的系统(系综)进行的实验来检验,因而玻恩几率解释让熟悉基于“决定论”的经典物理学的科学家颇不习惯,爱因斯坦和薛定谔等人据此对量子力学的哥本哈根诠释多次提出了尖锐的批评。
与以往批评不同,1935年,爱因斯坦(Albert Einstein)、波多尔斯基(Boris Podolsky)和罗森(Nathan Rosen)合作(图1),从一个新的角度对量子力学的哥本哈根诠释提出了批评。这一次爱因斯坦没有质疑量子力学的正确性,而是以佯谬的形式(Einstein—Podolsky—Rosen paradox,今称“EPR佯谬”)指出量子力学的不完备性。在题为《能认为量子力学对物理实在的描述是完备的吗?》的论文(下称“EPR论文”)中,他们借助检验两个粒子量子纠缠所呈现出的长程(非定域)关联性行为,突显定域实在性的要求与量子力学完备性之间的矛盾。

图1 EPR文章作者(从左至右):爱因斯坦(A. Einstein)、波多尔斯基(B. Podolsky)和罗森(N. Rosen)
以爱因斯坦一贯的、直面真理的学术风格,EPR的论述立足于严谨的思想观念、明晰的基本假设和缜密的逻辑方法,不像玻尔采用过度哲学化的、形而上的论述,使得人们无法用实验方法加以验证。爱因斯坦、波多尔斯基和罗森结合了当时被较多接受的物理理论定域性(locality)和实在性(reality)的观念,形成后来被称为定域实在论的物理观点。定域性(亦即爱因斯坦的可分隔性)是指:在给定区域发生的事件(原因)对其他区域的事件(结果)影响,只能以不超过光速的速度传递,从而不破坏时空因果关系。实在性要求,每一个可以通过“严格测量”确定的物理实在必须能在物理理论中找到对应的物理量,这时我们称这个理论是完备的。这里的“严格测量”是指在不干扰体系时原则上可精确测定对应于每一个物理实在的物理量的值。EPR佯谬的论证要点是基于波函数描述的量子力学不能满足定域性实在性的要求,从而是不完备的。
EPR文章是Podolsky根据三人讨论基础上“草就”和匆忙投稿的,爱因斯坦甚至认为文章有些曲解了他的本意。爱因斯坦并不强调实在性要素,他论证的关键是展示非定域性,即对于处于EPR态的粒子1中进行的任何力学量测量,都会导致粒子2的特定量子态。然而,由于狭义相对论的要求,粒子2的真实状态不能依赖于对类空(spacelike)距离上粒子1的测量,在这个意义上,量子力学波函数描述的不完备是由于它不能与真实物理状态一一对应。
针对EPR佯谬,1964年,约翰·贝尔(John Bell)(图2最左)石破天惊地作出了今天称之为“贝尔定理”的重要发现。他基于玻姆(David Bohm)的定域隐变量理论,推导出了特定纠缠态上关联测量满足的基本不等式——贝尔不等式。贝尔发现,量子力学关于这种关联的计算结果违背贝尔不等式,这展示了量子力学中必定存在非定域性问题,从而断定定域实在论不成立。量子力学已经是一个极为成功的科学分支,到1964年为止,量子力学预测的每一个结果都得到了实验证实。原则上我们无需进一步通过实验验证贝尔不等式的违背,但贝尔认为,量子非定域性展现的效应太鬼魅了,而且常常被误解为有“超距作用(或效应)”,而已有的相关实验检验只是旁证,因此有必要在非常严苛的条件下对贝尔不等式的违背直接进行实验验证,把量子力学最奇特的特征充分展示出来。诺贝尔奖评奖委员会在介绍2022年诺贝尔物理学奖的科学背景的结语中也强调了这个问题:“对大多数研究人员来说,原子和物理光学领域中充分的实验证据证实了量子力学的强大预测能力。因此,对他们来说,克劳斯和阿斯佩的实验并不令人惊讶(Indeed,the overwhelming empirical evidence in the realms of atomic and optical physics was,to most practitioners,confirmation of thepotent predictive power of quantum mechanics. Thus,to them,the experiments of Clauser and Aspect came as no surprise)”。后来的实验展示了在各种严苛的条件下量子力学的结果的确违背贝尔不等式,因此瑞典皇家科学院宣布将2022年诺贝尔物理学奖授予法国物理学家阿斯佩(Alain Aspect)、美国物理学家克劳泽(John F. Clauser)和奥地利物理学家塞林格(Anton Zeilinger)(图2右侧3人)。

图2 (从左至右)约翰⋅贝尔(J. S. Bell)以及2022年三位诺贝尔物理学奖获得者:阿斯佩(A. Aspect)、克劳泽(J. F. Clauser)和塞林格(A. Zeilinger)
贝尔不等式的提出和检验是量子力学基本问题研究的重要组成部分,相关探索持续了将近一个世纪,特别是在推动量子力学和信息科学交叉形成的前沿科技领域——量子信息方面起着关键的作用。在未来量子信息(包括量子通讯、量子计算和量子测量)的发展中,贝尔不等式相关的量子力学基本问题的研究是必不可少的。为了理解和阅读方便,本文的论述并不遵循贝尔不等式研究的历史进程,而是从经典关联和量子纠缠的差别入手,阐述什么是量子非定域性,通过“黑白球”的类比,讲清楚什么是定域隐变量理论,并推导出特定纠缠态上关联满足的贝尔不等式,得出量子力学对该关联的计算违背贝尔不等式这一结论。为了理解贝尔不等式,明确量子非定域性的物理意义,本文还介绍了EPR佯谬对量子力学诠释的挑战,并对量子力学是否与狭义相对论矛盾进行了详细的讨论。本文在介绍检验贝尔不等式的几个重要实验的物理动机和实验技术的递进情况时,不仅介绍了吴健雄、李政道、杨振宁等前辈华人科学家对该领域的早期贡献,而且特别强调了陈创天等人发现的BBO等非线性晶体在产生EPR纠缠光子态的关键作用,以及史砚华、欧泽宇和彭堃墀等人利用这些晶体产生量子纠缠和检验贝尔不等式违背的实验工作。
量子纠缠与量子非定域性——大尺度上的量子效应
量子纠缠的观念起源于EPR佯谬的讨论。1935年,爱因斯坦等人首先写出连续变量的量子纠缠态——EPR态|EPR>(Box 1),不久后,薛定谔据此总结出量子纠缠态的概念:对于二粒子(两部分)复合系统,不能写为因子化形式的状态

被称为量子纠缠态(entanglement)。1950年前后,玻姆(David Bohm)建议在讨论EPR佯谬时使用离散变量的EPR纠缠态,今天也被称为贝尔态。这个态是两个自旋粒子系统的纠缠态:

它可以更加清楚地说明两粒子测量结果关联问题。
表1 贝尔态自旋关联测量的结果

在一个贝尔态上分别测量两个粒子的z方向自旋会得到如表1第一部分所示的关联结果。假设两个粒子相隔一段距离d,甲乙两位观测者分别测量粒子1和2,当甲观察到粒子1处于自旋向上的态时,乙通常观察到粒子2处于自旋向下的态,如此等等。
然而,在事先给定了基矢作为测量的参照标准的情况下,上述的关联与以下的经典关联事件没有本质区别:甲与乙2人约定在一个暗盒里放两个球,他们事先知道是一黑一白。甲从中摸出一个球,不看它是什么颜色就带它离开远行,不管他走多远,一旦他发现所持之球为黑,瞬间即知留在乙处暗盒里的球是白色的,反之亦然,这种关联如表2所示。
表2 两体经典事件的测量值关联和隐变量

显然,看上去知道白球的“信息”是超光速的,但这种关联是平凡的。然而量子态所代表的关联远不止于这些,它包含各种关联,具有关联的多样性。这是因为,同样的两自旋系统的贝尔态|B>还可以表达为

它代表方向的关联,这里

事实上,自旋在单位矢量上的投影

的本征值为±1,本征函数记为


其中,

自旋极化角度可以形象地理解为自旋的“颜色”。如图4所示,同一个态|既可以代表“黑—白关联”,也可以表示“蓝—黄关联”或“红—绿关联”。

图4 量子纠缠的关联多样性
现在我们用关联函数定量地描述纠缠态代表的量子关联多样性。我们可以对自旋1和自旋2进行方向不一致的测量——对自旋1测⋅,对自旋2测⋅(≠),这两种测量结果之间的关联如何描述?对任意的和,这种测量没有直接的经典对应,但量子力学可以用关联量

给出问题的精确描述,即测量关联函数



显然,两个自旋不论相距多远,只要a·b≠0(不正交),它们在a和b上投影测量结果就是关联的。双方都测z(或x)方向自旋。当测量的两个方向相垂直,则关联函数为零。形象地说,探测粒子1在z方向自旋,相应地考察粒子2沿x方向自旋,一旦观察到粒子1有z方向极化,则粒子2就没有沿着x方向的关联极化。
如图5所示,在类空距离上,两自旋非零的长程关联Q(a,b )代表了量子力学特有的非定域性。这种非定域性在量子多体系统中很常见,如超导和玻色—爱因斯坦凝聚中的非对角长程序,但是否出现在类空的距离上,当时实验上并无答案。然而,量子非定域性并不意味着超光速的“超距作用(效应)”(action at a distance)。在类空距离上两个力学量关联函数≠0,只是意味着“测量”A确实会影响B的“测量”。关联函数所涉及的均为对期望值的测量,并没有对波函数变化采用波包塌缩的假设,更不涉及传递信息或能量的单粒子事件,关联之间的关系只是反映了统计平均的结果,并不违背狭义相对论。正如罗森后来回答别人对EPR论文批评时指出,爱因斯坦等坚持的定域性要求虽然是一个“错误假设”,但文章没有错。提出这种佯谬是不平庸的,它引发了纠缠态概念的诞生,导致了贝尔不等式的发现,使得人们能够更加深刻地理解量子力学。

图5 纠缠对的非局域关联:在类空距离上两个力学量A和B的关联函数
BOX 1
连续变量EPR态
它是

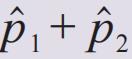
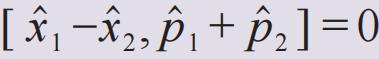

它有两种分别基于动量本征态
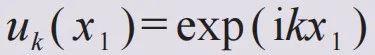



BO
我们可以用贝尔不等式定量地表征上述的量子非定域性,考察量子力学期望值对于经典系综“隐变量”平均结果的偏离。这种非定域性看上去可能有某种经典的起因,也就是说存在某种经典不可见的变量(“隐变量”)把“超距”的测量结果关联在一起。然而,贝尔在1964年的一篇文章中否定了这种经典“隐变量”的存在。考虑在,和三个方向测量自旋,他发现依据量子力学计算的关联完全不同于隐变量理论给出的结果,这使得人们能够在实验上判定是否存在定域隐变量。后来,实验物理学家进行了贝尔不等式相关的实验(见第6节),实验结果否定了定域隐变量理论对“超距”关联的解释。
根据“黑—白球”暗盒的经典关联类比,事先知道了盒中有黑白两球。甲乙取黑或取白完全由的值决定(表2)。一般地说来,也可以连续取值,上述关联效应有如图6所示的形象展示,其中经典“自旋”取连续的方向:用方向角刻画隐变量,粒子沿方向的自旋的测量值由隐变量决定。局域性表现在只是的函数,与它的积分过程无关。参数及其分布在粒子分离前就给定了,不存在非定域性,通常取值可以不确定,在经典意义下可以是随机的,其分布函数满足:


图6 隐变量连续取值对应的自旋关联
显然,上述的隐变量理论力图把量子力学描述为与经典统计力学类似的概率性统计理论:力学量的取值由隐变量的值决定,只是由于某种技术的限制,无法准确地确定和相应力学量的值,因而只能退而求其次,研究这些力学量的隐变量概率分布()。如同经典统计力学,它认为其研究对象(如大量气体分子)的位置、速度等力学量都有确定的取值,但由于技术的限制,无法对它们进行准确地计算和测量,而只能研究其取值的概率分布。这样的理解显然非常符合人们的直觉。如果一个物理系统包含两个或多个处于空间不同位置的粒子(两个粒子的距离为),人们在讨论量子力学和隐变量理论的关系时,会很自然地要求隐变量理论满足狭义相对论的要求,即,如果对一个粒子进行了一次测量,那么在测量后小于/的这段时间内(是光速),该测量不会对另一个类空距离上的粒子产生任何影响,当然也不会改变另一个粒子的力学量的取值。满足这种“爱因斯坦分隔性”要求的隐变量理论称为“定域隐变量理论”。
1964年,贝尔基于隐变量处理计算出粒子1和2分别沿和测量值的关联:

再考虑到更多方向的自旋测量关联,得到著名的贝尔不等式(证明见Box 3)

然而,量子力学计算给出的量子关联与上面的结论是矛盾的。设a,b,c在一个平面内,夹角依次差60°,则根据量子力学的计算:

因而,

对照贝尔不等式,量子力学的结果显然与之矛盾,后来的各种实验也支持量子力学的结果,从而进一步证明了定域隐变量理论不成立。其实,对于处在空间不同位置的两个自旋1/2粒子(称为1和2),一个定域隐变量理论给出的结果必然满足贝尔不等式,而量子力学给出的结果可能会违反该不等式,因此不存在与量子力学等价的定域隐变量理论。

图7 李政道和杨振宁
最近我们调研文献发现,李政道和杨振宁(图7)在1960年初就意识到,量子力学中的关联与经典关联有着本质的差别。李政道在阿贡(Argonne)国立实验室访问时谈到他们关于量子力学在宏观尺度上关联效应的工作。他指出,这些关联效应存在于同时产生并向相反方向运动的两个中性K介子


图8 Day在1961年发表的文章中提及了李政道和杨振宁对于EPR佯谬的讨论
BOX 3
贝尔不等式的证明
我们计算


而


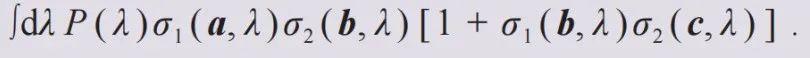
它的绝对值最多等于绝对值的积分,且


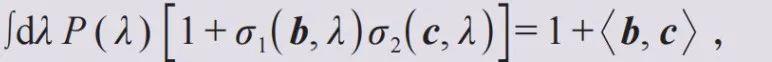
从而有贝尔不等式。
EPR佯谬与量子力学诠释的波包塌缩
自量子力学诞生之日起,量子力学的哥本哈根诠释就遭到了爱因斯坦和薛定谔等人的责难。值得注意的是,1935年爱因斯坦等人所质疑的并不是量子力学本身的正确性,而是基于玻尔哥本哈根诠释的“量子力学”(本文中带引号的“量子力学”都特指包含了波包塌缩假设的量子力学)是否完备。根据这种“量子力学”的观点,波函数给出了我们关于微观世界的全部知识,但波函数与实际实验的联系,必须借助于量子力学外部的经典世界——如经典仪器,测量后测量仪器(或观测者)引起的波函数塌缩到待测量力学量的本征态上,由此得到关于量子系统的知识。这种测量称为投影测量,它是一个量子力学自身不能刻画的非幺正过程。然而,包括爱因斯坦、薛定谔、温伯格乃至贝尔在内的很多物理学家对此都从不同的角度提出了严厉的批评。
爱因斯坦、波多尔斯基和罗森认为,物理理论必须满足以下两个条件:(a)物理理论的正确与否取决于物理理论的预测与实验结果的符合程度;(b)物理理论必须给出对象系统完备的描述。量子力学显然满足条件(a),其预测与所有实验结果之间没有什么明显矛盾,但量子力学是否完备,这正是EPR文章质疑的核心问题。对此,爱因斯坦等首先对分析问题所涉及的两个概念给出了严格定义:(1)物理实在(reality):若在对于系统不造成任何扰动的情况下,能以等于1的概率准确地预测物理量的数值,则存在对应于这物理量的物理实在的要素;(2)完备性(completeness):物理实在的每个要素都必须在物理理论里有其对应部分。根据玻姆等人的分析,EPR的论证过程还隐含了以下的假设:(i)世界能够正确地分解为一个个独立存在的“物理实在的要素”;(ii)定域性:如果两个系统相互作用产生关联态后分开距离足够远(类空),对其中一个系统的任何操作,都不会引起第二个系统的任何实质性变化;(iii)EPR在推断多个要素构成物理实在时,明显地使用了量子力学哥本哈根诠释的标志性假设——波包塌缩(或叫波函数约化)(…the second system is left in the state given by the wave function corresponding to the eigenvalue…. This is the process of reduction of wave packet …)。需要指出的是,因为这个假设,量子非定域性才隐喻了“超光速”的“超距作用”的结论。

图9 二自旋贝尔态的关联测量
我们以图9所示的二自旋系统为例说明什么是物理实在和怎样依据假设(i)—(iii)描述它,以及量子力学的完备性。甲、乙两人分别对一定距离上的处于纠缠态|>上的两个自旋体系进行测量。根据假设(iii),在哥本哈根诠释的意义下,测量是投影测量,测量后导致波包塌缩。例如,由于





表3 二自旋贝尔态上和的关联测量结果

当然,也有人质疑EPR推理分析中物理实在的假设,认为物理实在是相对的:对乙来说,和不是同时存在的物理实在,但对于遥远的甲来说,和同时却是共存的物理实在(Box 4)。然而,这种相对主义的做法,使得什么是量子力学物理实在的问题解答更趋向主观主义的观点,因为实在性问题依赖于不同的观察者。
现在我们再一次强调,爱因斯坦等所质疑的量子力学不完备是特指哥本哈根诠释加持下的“量子力学”:波函数描述单粒子的物理实在,测量力学量一旦确定了随机结果中的一个,则波函数会塌缩到对应的本征态上。由此推理,如果这个粒子是复合系统的一部分(剩余部分为),则关于的塌缩过程也会引起的同步塌缩。然而,在贝尔不等式违背的理论和实验分析中,从未涉及具体的波包塌缩的问题,所有的讨论只是关于各种期望值的量子力学计算。因此,不管是隐变量的讨论,还是量子力学关于关联函数的计算,原则上不涉及任何实际发生的塌缩过程。从这个意义上讲,类空点间关联函数不为零,只是代表了量子力学中存在非定域性,从逻辑上无法推断这就是超光速的“超距作用”。
最后我们指出,摒弃波包塌缩假设,虽然使得人们无法通过类空距离上的遥测来确定“物理实在”,但却可以避免物理实在依赖观测者的主观主义,从而维护量子力学的内在自洽性。从量子力学完备性的角度讲,不采用波包塌缩的假设,就不能由粒子1的测量结果以1的概率准确获得粒子2的知识,物理实在的要素被大大缩减了,可能不太“完备”了。然而,在这种情况下,虽然付出的代价是承认量子力学理论的物理实在要素数目少于对应的经典物理实在要素的数目,但前面的与狭义相对论的矛盾却被彻底克服了,理论的自洽性也得到了保障,类空距离上量子关联函数非零且可突破贝尔不等式限制的量子特性从而被明确地突显出来,导致了关于检验量子力学适用性的基础物理实验——贝尔实验(Bell experiment)。
BOX 4
物理实在的一般操作定义
考虑粒子1和粒子2构成的双粒子复合系统。设



相互作用使得这个复合系统在短时内演化到纠缠态(施密特分解):

然后两个粒子分开足够远,以至于距离是类空的。当集合{}中至少有2个非零,则意味着两个系统存在某种关联,即一旦指定对测量者甲测量得到确定的值,系统整体地塌缩到基矢量

表4 两体纠缠态的测量值关联

然而,若测量粒子1的另一个力学量','的本征态{|'>}展开同一个态:

其中{|'>}对应于另一个粒子2的力学量',这个测量可以准确地得到其本征值为',因而B'也是粒子2的物理实在,因此在甲看来和'同为物理实在。然而,在很多情况下,[, ']≠0,因而在乙看来,和'不再同时是粒子2的物理实在,因为由不确定性关系可知B的准确测量将排斥对B'的准确测量。
贝尔不等式的推广与GHZ态
贝尔的文章发表后,包括获得2022年诺贝尔物理学奖的克劳泽和塞林格在内的很多人将贝尔的结果进行了推广,从理论上研究了各类不同系统和不同情况下的定域隐变量理论,展示了它们与量子力学的矛盾。贝尔不等式第一次将局域隐变量理论转变成了一个可用实际实验验证的科学理论。
然而,若直接以贝尔不等式为对象进行实验检验则会存在实现上的困难。观察贝尔不等式方程(11)的两边可以发现,该不等式的左边要求实验者乙一侧的方向参数必须调至,不等式右边却要求实验者甲一侧的参数也要同样地调至,这将导致以下两个实验逻辑上的问题:(1)同时调整距离很远乃至类空的两个仪器的参数匹配至完全一致,不仅在实际上是不现实的,在原理上也是不允许的(不能交流信息);(2)贝尔曾强调了“在粒子飞行过程中改变测量仪器设置”的重要性。在类空距离上同步设置操作仪器,才能确保偏振器之间没有任何直接信号交换。为了在现实实验中检验形式如式(11)的贝尔不等式,两个实验者即使允许及时传递两侧仪器的参数信息,以同步调控得到精确一致的方向参数,在技术上这也是一个十分困难的任务。
为了克服这个困难,克劳泽,M. Horne,A. Shimony和R. Holt等四人在1969年给出了贝尔不等式的一个更便于实验检验的版本——CHSH不等式。该不等式也适用于处于空间不同位置的两个自旋1/2粒子1和2。

注意上式对所有的隐变量值λ均成立。因此,将上式乘以隐变量概率分布()并积分,就得到:

这就是CHSH不等式。检验这个不等式并不要求同时调节两侧仪器有某个相同参数,使实验验证定域隐变量理论变得更加现实。注意CHSH不等式对于任何定域隐变量理论也都成立。
另一方面,基于量子力学的计算则预言:该不等式可能被违反。例如,在系统处于自旋单态时,如果选择和分别为方向和方向的单位矢量,和分别为平面上与轴夹角为π/4和3π/4的单位矢量(图10),则量子力学计算给出



图10 量子力学给出的会违反CHSH不等式的自旋方向
人们还进一步认识到,除自旋单态外,很多其他的量子态中也都能出现量子力学和定域隐变量理论的矛盾,也表现为各种各样的贝尔不等式的推广。1980年代末,Greenberger,Horne和塞林格还发现对于包含3个或更多粒子的系统,定域隐变量理论和“量子力学”的矛盾可以表现得更加尖锐,甚至不需要借助类似于贝尔不等式的不等式和统计平均(Box 5)。
BOX 5
GHZ态及其非定域性
考虑三个粒子(记为1,2,3)的GHZ态:

它满足:


即,当系统处于GHZ时,三个力学量






这里,和分别为,和方向的单位矢量,(, )(=1,2,3)表示粒子的力学量




这意味着,要满足上述条件,必然有



此时,根据量子力学,当系统处于GHZ时力学量


贝尔不等式的实验检验
上述贝尔不等式相关的理论工作表明了量子力学不可能等价于一种定域隐变量理论。微观世界的真实物理规律究竟是满足量子力学还是满足定域隐变量理论?在贝尔不等式提出之前,这只是一个形而上学(metaphysics)的问题,人们只能进行哲学层面上的争辩和讨论,但有了贝尔不等式及其推广,人们就可以通过进一步的实验来回答这一重要问题。
2022年诺贝尔物理学奖授予了验证贝尔不等式违背的一系列实验工作:利用双光子纠缠态检验CHSH版本的贝尔不等式。此类实验通常选择光子的偏振充当赝自旋自由度,即将光子的水平偏振态|>和竖直偏振态|>分别作为赝自旋的|↑>和|↓>态,而对各个不同方向的赝自旋的测量则等价于对不同方向的光子偏振的测量。如图11所示,此类实验包含以下基本步骤:纠缠源S产生两光子赝自旋纠缠态|>,之后将两个光子1和2分别发送到Alice和Bob的两地。Alice通过调整偏振片可以选取和中随机的一个方向,记为;Bob调整他的偏振片从和中随机选择一个方向,记为。平行于偏振片方向的光子透射并被探测器捕捉,垂直于偏振片方向的光子被反射并被探测器捕捉。上述Alice和Bob处的“随机选择 测量”的时间间隔应小于/,其中为Alice和Bob两地的间距。所谓的符合探测(coincidence detection)是指,给定延迟时间间隔,如果探测器接收到两个光子,则有一个计数,相当于两个测量结果相乘。重复上面步骤多次,得到大量测量结果。将每个量的测量结果各自进行统计平均,即得到



图11 基于光子符合测量的CHSH不等式实验检验示意图
要完成这类基于量子纠缠的实验,首先要制备处于理想纠缠态上的光子对。1948年,惠勒提出,正负电子湮灭时会产生一对具有不同偏振方向的光子。这对光子就处于偏振纠缠态。1950年,吴健雄和萨科诺夫在电子对湮灭实验中观测到了这种光子对(图12)。这对光子由具有零角动量的正、负电子对湮没后发出,互成直角而被极化。这一结果也证明正电子与负电子的宇称相反。

图12 1950年吴健雄和萨科诺夫在电子对湮灭实验中观测到了纠缠光子对
1967年,C. A. Kocher和E. D. Commins用紫外光照射钙原子(图13),使外层电子跃迁到高激发态,然后通过级联自发辐射发出一对波长分别为5513 Å和4227 Å的光子。根据选择定则,当这对光子的动量方向刚好相反时,它们要么都处于水平偏振|H>,要么都处于竖直偏振|V>,也可以处于纠缠态


图13 级联辐射方法制备纠缠光子对
1972年,克劳泽及其合作者利用这种级联辐射的方法制备纠缠光子对,完成了第一个前述类型的CHSH不等式检验实验。实验结果明显违反CHSH不等式,这意味着量子力学不能用隐藏变量理论取代。然而,该实验中还存在所谓的局域性漏洞。该实验只有一个光子传输的通道,实验中所测量的光子偏振方向一旦确定,就在之后对大量光子对的测量中都无法更改,并未如前所要求的那样在对每对光子进行测量前都随机确定,这时Alice和Bob中间可能会有事先的经典关联信息。
1981—1982年,阿斯佩及其合作者进一步完成了三个CHSH不等式检验实验。在这些实验中,他们将照射钙原子的紫外光改为激光,从而增加了纠缠光子对的制备效率,并将Alice和Bob两地的间距增大到了13 m左右(对应光速飞行时间/约为40 ns)。更重要的是,在第三个实验中,阿斯佩等人利用声光开关装置快速改变Alice和Bob处测量的光子赝自旋方向,如图14所示,这个实验本质上是一个四通道的实验。在这个实验中,每个声光开关(C1,C2)利用不同频率驻波控制入射光子走两个不同的通道,每个通道中的偏振片极化方向不一样,意味着测量不同的光子赝自旋。声光开关可以以25—50 MHz的速率快速切换光子所走的通道,即改变测量方向和的选择,改变一次的时间约为10 ns,因此做到了对每个光子进行测量前(即光子从光源到Alice或Bob处的飞行途中)才临时确定所测的偏振方向,从而很大程度上避免了前述局域性漏洞的出现。阿斯佩等人在实验中观测到了对CHSH不等式的更为显著的违背,进一步确认微观世界的规律不能被定域隐变量理论重新描述。

图14 阿斯佩及其合作者的实验装置示意图
如果说克劳泽检验贝尔不等式的实验是第一代的,阿斯佩的实验则是属于第二代的,它最成功地展示了量子力学结果对贝尔不等式违背了数个标准差。不过需要指出的是,阿斯佩等人的上述实验并未彻底解决局域性漏洞。这是因为实验中Alice和Bob处所测的光子偏振方向虽然随时间快速变化,但其变化方式却是事先确定好的(赝自旋方向以设定的频率周期性变化,虽然Alice和Bob处的变化周期是非公度的,但仍有规律可循)。因此该实验并未做到要求的“Alice和Bob各自在每次测量前才随机选择所测的偏振方向”,且在每对光子的实验中,“Alice做选择”和“Bob做选择”这两个事件时间间隔小于d/C。
按照阿斯佩的说法,第三代测试于20世纪80年代末在马里兰和罗彻斯特开始,人们使用了紫外线光在特殊晶体上的非线性光学效应——参量下转换产生相关的EPR光子对。有了这样的纠缠光子对,纠缠的变量既可以是玻姆和贝尔使用的、类似于自旋分量等离散变量的光偏振,也可以是爱因斯坦、波多尔斯基和罗森最初建议的那种连续变量。需要指出的是,20世纪80年代,中国科学院福建物质结构研究所陈创天及其团队发现了低温相(相)硼酸钡晶体(-BaBO,简称BBO晶体),这是一种使用广泛的非线性光学晶体,它是产生纠缠光子对的关键性材料。后来,基于非线性光学晶体中的参量下转换过程(图15),纠缠光子对的制备技术又获得了极大发展,进一步推动了贝尔不等式的实验检验研究。

图15 BBO晶体产生纠缠光子。纠缠光子对是当激光束通过一块晶体(比如BBO晶体)时产生的。晶体有时会把单一的一个紫外光子转化为两个具有更低能量的光子,一个是竖直偏振(在红色圆锥上),一个是水平偏振(在蓝色圆锥上)。如果光子恰好沿着圆锥交线处传播(绿色),这两个光子都不会有确定的偏振,但是他们的相对偏振是补偿的,处于偏振纠缠态,彩色图像(右图)是下转换光的图像。彩色不代表光的颜色。
1988年,史砚华(图16)和Alley利用非线性光学晶体KDP(磷酸二氢钾)中具有第一类(type-I)位相匹配条件的参量下转换过程产生了一对频率相同但传播方向不同的光子,并将其制备在两个正交的偏振态上(以下以水平偏振态|H>和竖直偏振态|V>为例),之后令这两个光子同时到达一个分束器(beam splitter,简称BS)的两侧。两个光子通过分束器后,有可能从同一侧出射,也有可能从两侧分别出射。容易证明,如果这两个光子从两侧分别出射,则出射后它们会处于偏振纠缠态


图16 早期与纠缠态贝尔实验密切相关的华人学者:陈创天、史砚华、彭堃墀、欧泽宇和潘建伟(从左到右)
1995年,P. G. Kwiat、塞林格和史砚华等人进一步提出利用BBO晶体中具有第二类(type-II)位相匹配条件的参量下转换过程,不借助分束器而直接制备偏振纠缠光子对的方法。BBO晶体在泵浦光的作用下可以发出两个偏振方向相互垂直的光子。当这两个光子的传播方向刚好位于一个特定平面时,可以利用史砚华等人1994年提出的光程补偿技术,使出射的光子进行处于偏振纠缠态

最后,我们总结一下上述几个关键贝尔不等式违背的实验检验工作的各自特点和面向科学需求的技术改进:克劳泽发展了第一个实际的贝尔实验(图17(a)),实验结果明显违反贝尔不等式,从而支持了量子力学,也就意味着量子力学不能被使用隐藏变量的理论所取代。阿斯佩进一步发展了这一实验(图17(b)),在光子离开信号源的飞行中,快速切换测量方向,弥补了局域性漏洞。塞林格科研组开始使用非线性晶体产生纠缠光子对以及随机数发生器来切换测量装置(图17(c)),进一步关闭了局域性漏洞。另外,塞林格科研组成功进行了量子隐形传态的演示实验,可以将量子态从一个粒子转移到远距离的另一个粒子。在这个基础上,塞林格科研组进行量子通讯的演示实验,潘建伟参与了早期工作,回国后开始了5光子纠缠和更多量子通信的实验研究。

图17 贝尔不等式违背的实验检验工作 (a)克劳泽发展了第一个实际的贝尔实验,实验明显违反贝尔不等式,从而支持了量子力学;(b)阿斯佩进一步发展克劳泽等的实验,在光子离开信号源的飞行中,快速切换测量方向,弥补了局域性漏洞;(c)塞林格科研组开始使用非线性晶体产生纠缠光子对以及随机数发生器来切换测量装置,进一步关闭了局域性漏洞。
结论与评述
以上我们简要地介绍了贝尔不等式的提出背景、科学思想发展和相关的实验研究,对2022年诺贝尔物理学奖进行了科学普及性的解读。在本文结束前,我们再探讨一下与贝尔不等式相关的量子力学基本问题的理解,以澄清一些常见的对贝尔不等式意义基于直觉的误解。
(1)贝尔不等式违背是否需要实验验证?
1982年阿斯佩的实验重新复苏了人们对于EPR佯谬、隐变量理论、贝尔不等式相关的量子力学基本问题研究的兴趣。英国广播公司为此专门采访了贝尔、阿斯佩和玻姆等许多学者,采访中特别提及“贝尔不等式是否还需要实验验证”等敏感问题。在2022年诺贝尔奖提供的专业背景材料中也提到了类似的问题:“对大多数研究人员来说,原子和物理光学领域中充分的实验证据证实了量子力学的强大预测能力。因此,对他们来说,克劳泽和阿斯佩的实验并不令人惊讶。”当年贝尔也承认,实验上违背贝尔不等式并不奇怪,因为它是已经被大量实验证实的量子力学的直接逻辑推论。然而,贝尔不等式所展示的量子非定域效应太“鬼魅”(spooky)了,存在类空距离上的关联,这是宏观大尺度上的量子效应,比超导、玻色—爱因斯坦凝聚等宏观效应更令人惊奇。过去的实验展示和验证相关的效应只是一种旁证,现在有必要在更苛刻的条件下、在更大的尺度上佐证量子力学的成立(Previously we were just relying in a way on circumstantial evidence. Quantum mechanics had never been wrong. And now we know that it will not be wrong even in the severy tricky conditions)。
(2)在量子纠缠态上,类空关联测量意味着“超光速”吗?
同样是在英国广播公司的那次采访中,他们问阿斯佩“那么你是否相信有可能在不同的区域之间产生了某种比光还要快的信号呢?”阿斯佩的回答是:“不,我不认为会有某种信号,如果你所说的信号是指有某种真正的信息传递的话。”然而,很多介绍量子纠缠以及贝尔不等式的文章中常见的一种说法是:“两个粒子1、2分处A、B两地,A地的人只要测出粒子1的状态,就立刻可知粒子2的状态,尽管他没到B地”。如果这句话暗含着超光速的意思,这个说法是有错误的。事实上,上面引号中所描述的事实有“超距作用”并无任何神奇之处,本文第二节讨论的“黑球—白球”信息预设关联导致“超光速”的讨论就是这样的例子。虽然“爱因斯坦分隔区”之间的测量相互影响,但绝没有信息能量超光速传递,这正是量子非定域性的绝妙之处!定域隐变量理论给出的自旋关联必然满足贝尔不等式,而量子力学给出的结果却有可能违反该不等式。换句话说,当两个粒子处在量子纠缠态时,其自旋关联的值会突破定域隐变量理论的限制,而这种情况在经典世界是绝对不会出现的。这才是量子纠缠态的特殊性质。
(3)质疑“量子力学”的EPR文章被证伪了吗?或爱因斯坦错了吗?
EPR佯谬之所以称之为佯谬(paradox或悖论),因为它包含一种前提假设有矛盾的命题。贝尔原始文章的题目就是“关于EPR佯谬”。正如罗森回答Mermin批评时说,“论文没有错,它做了一些假设,然后得出逻辑结论;这些假设有错误。”在EPR的文章中,爱因斯坦等在论证如何得到“物理实在”时,假设了所谓的“爱因斯坦分隔性”(“定域性”):在类空距离上遥测不影响测量对象的状态,但在讨论物理实在时却使用“量子力学”的哥本哈根标志性“假设”——波包塌缩,而整体的波包塌缩恰恰破坏“爱因斯坦分隔性”。或许,这就是罗森所说的“假设是错误的”。其实,早在发现贝尔不等式之前玻姆就指出了这一点:EPR佯谬的出现是因为爱因斯坦等把整体性的微观世界解构为一个个独立存在的要素,分隔成因果不相关多个部分。爱因斯坦等自己采用波包塌缩假设破坏了自己要求的“爱因斯坦可分隔性”——定域性,这正是EPR佯谬的要害所在!
(4)“大贝尔实验”比以前的贝尔实验进步了多少?
为了更好地验证贝尔不等式的违背,人们希望完全随机地改变滤波片的方向,但实验中使用的随机数无法做到真正的随机(即伪随机),为了填补随机数上的漏洞,2016年开始,来自11个国家的13个实验小组联合完成了一次“大贝尔实验”。该实验的基本思想是:用大量独立志愿者替代物理随机数产生器,从而让实验中每次测量的光子偏振方向的随机选择更加统计独立。在实验中,全世界约10万名志愿者各自独立地通过手机游戏等方法随机发送“0”和“1”给所有实验小组。13个实验小组全都根据收到的数据确定各自实验中所测量的光子偏振方向(或其他等效自旋1/2系统的赝自旋方向)。实验总计历时约51小时,在最高峰的12小时,志愿者每秒产生约1000个数据。13个实验小组全都观测到了对贝尔不等式的违背。大贝尔实验主要是一个科普性质的实验。然而,值得反思的是,为了克服局域性漏洞而强化随机性要求的“大贝尔实验”本质上也存在局域性漏洞的新问题:位于世界各地的志愿者发送的随机数要通过互联网传送,且要先经过一些中继点进行汇总后再发给实验者(中继点约每2 s发送一批数据给实验室),因此“志愿者决定发送某个数据”和“实验室根据该数据进行赝自旋测量”这两个事件之间的间隔时间,大于光子从志愿者运动到实验室的时间。实验的组织者在文章中直接承认了这个问题:在实验中“人的选择和测量之间不能构成类空间隔(human choices are too slow to be space-like separated from the measurements)”。因此,如何科学地评估和支持“大贝尔实验”这类实验,是考量基础科学发展策略的典型案例。
致 谢 本文作者孙昌璞感谢与傅立斌教授、董辉研究员、李颖研究员和马宇翰博士的讨论,以及彭堃墀、资剑和张靖三位教授的意见与建议。
参考文献
[1] Einstein A,Podolsky B,Rosen N. Physical Review,1935,47:777
[2] Harrigan N,Spekkens R W. Foundations of Physics.,2010,40 (2):125
[3] Bell J S. Physics Physique Fizika,1964,1:195
[4] Bohm D. Physical Review,1952,85:166
[5] Scientific Background on the Nobel Prize in Physics 2022. https://www.nobelprize.org
[6] Schrödinger E. Mathematical Proceedings of the Cambridge Philosophical Society,1935,31(4):555
[7] Bohm D. Quantum Theory. Englewood Cliffs,NJ:Prentice-Hall,1951
[8] Peres A. Foundations of Physics,2005,35(3):511
[9] 马克斯·雅默. 量子力学的哲学. 商务印书馆,1989
[10] Day T B. Physical Review,1961,121:1204
[11] Clauser J F,Horne M A,Shimony A et al. Phys. Rev. Lett.,1969,23:880
[12] Wu C S,Shaknov I. Physical Review,1950,77:136
[13] Kocher C A,Commins E D. Phys. Rev. Lett.,1967,18:575
[14] Freedman S J,Clauser J F. Phys. Rev. Lett.,1972,28:938
[15] Aspect A,Grangier P,Roger G. Phys. Rev. Lett.,1981,47:460
[16] Aspect A,Dalibard J,Roger G. Phys. Rev. Lett.,1982,49:1804
[17] Aspect A,Grangier P,Roger G. Phys. Rev. Lett.,1982,49:91
[18] Aspect A. Nature,1999,398:189
[19] Shih Y H,Alley C O. Phys. Rev. Lett.,1988,61:2921
[20] Ou Z Y,Mandel L. Phys. Rev. Lett.,1988,61:50
[21] Ou Z Y,Pereira S F,Kimble H J et al. Phys. Rev. Lett.,1992,68:3663
[22] Kwiat P G,Mattle K,Weinfurter H et al. Phys. Rev. Lett.,1995,75:4337
[23] Weihs G,Jennewein T,Simon C et al. Phys. Rev. Lett.,1998,81:5039
[24] Bennett C H,Brassard G,Crépeau C et al. Phys. Rev. Lett.,1993,70:1895
[25] Bouwmeester D,Pan J W,Mattle K et al. Nature,1997,390:575
[26] Davies P W,Brown J R. The Ghost in the Atom. Cambridge University Press,1986
[27] The BIG Bell Test Collaboration. Nature,2018,557:212
转载内容仅代表作者观点
不代表中科院物理所立场
如需转载请联系原公众号
来源:中国物理学会期刊网

编辑:小聪
,





