
关注“中考数学当百荟”,感谢您的点赞,转发!点击“了解更多”
北师大版《数学》九上P187有一道习题:任意说出3个正数,以这3个数为边长一定能围成一个三角形吗?一定能围成一个钝角三角形吗?请设计一个试验估计围成一个钝角三角形的概率.一.以任意3个正数a<b<c为边长,围成钝角三角形的条件是什么?3个正数为边长围成三角形的条件:a+b>c,这是大家都知道的,但是要围成钝角三角形则啊a,b,c满足什么条件呢?让我们先回顾围成直角三角形的条件:a^2+b^2=c^2,此时,c边所对的角最大且为直角。
显然当a^2+b^2≠c^2时,c边所对的角最大,但非直角!
追问一句,此时,不是直角是什么角?
——锐角或钝角。
——好的!从角的分类来说只有三种情况:锐角、直角、钝角。排除一种(直角),当然还有两种可能。那么a^2+b^2与c^2,其值的也有三种情况:小于、等于、大于。排除一种(相等),势必也有两种可能:小于或大于。
自然联想到它们之间的达成某种默契:

结论
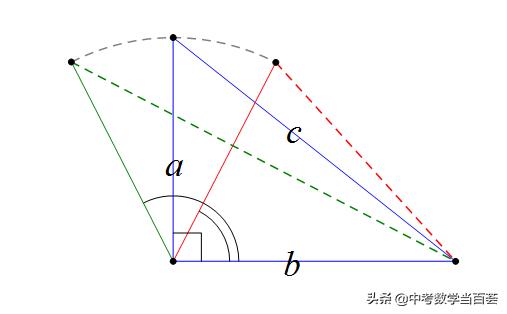
以任意三个正数0<a<b<c为边长,围成钝角三角形的条件:a+b>c,a^2+b^2<c^2.
二.换一个角度再解读围成钝角三角形的条件:a+b>c,a^2+b^2<c^2.弄清楚围成钝角三角形的条件后,我们是不是迫不及待地进行试验啦?
当然是可以的,不过可以预见试验的效度、信度肯定不高。没有更好的办法呢?让我们继续探究下去,或许可以找到更好的办法。
围成钝角三角形的条件:a+b>c,a^2+b^2<c^2.
将这两个不等式进一步变形(右边都变成“1”)得
a/c+b/c>1,(a/c)^2+(a/c)^2<1
设x= a/c,y= b/c,则有x+y>1,x^2+y ^2<1,其中0<x<1,0<y<1.
让我们从函数的角度,再来解读围成钝角三角形的条件:
x+y>1的含义:x+y=1表示直线y=-x+1上所有点,若x+y≠1,则表示直线外的所有点,这个描述显然还不够“精细”,自然想到x+y≠1,意味着x+y<1或x+y>1,其含义必然对应着直线的下方与下方(的所有点组成的区域).
类比联想
x^2+y ^2<1,x^2+y ^2=1(圆心在坐标原点,半径为1的圆),x^2+y ^2>1,也有类似的含义(见下表).

解读围成钝角三角形的条件:x+y>1,x^2+y ^2<1,其中0<x<1,0<y<1的含义:
直角坐标平面内,0<x<1,0<y<1,即正方形区域(0,0)(1,0),(1,0)(1,1)的内部(不包括边界);x+y>1,即直线y=-x+1的上方;x^2+y ^2<1,即圆心在原点,半径为1的圆形区域内部。所以围成钝角三角形的条件就与这三个区域的公共区域内(如图所示的弓形区域,不包括边界)的随机点的横、纵坐标相关(即以该区域内任一点的横坐标= a/c,纵坐标= b/c)。

画一个边长为1的正方形,再以一个顶点为圆心,边长为半径画弧(1/4圆周),并连结弧的两端(正方形的一条对角线)向这个正方形内随机投掷骰子,分别统计投掷骰子落在正方形区域的次数m, 骰子落在弓形区域的次数n,计算出骰子落在弓形区域的频率n/m,按统计(用频率估计概率)原理,这个频率n/m就是以任意3个正数为边长围成钝角三角形的概率.
用电脑模拟这个试验,试验结果(如图)


1.从以任意三个正数为边长围成三角形、钝角三角形的概率问题转化到向一正方形区域掷骰子问题,这个思维跨度是非常大的,对学生来说不亚于一次时空穿越,带给他们感受是非常震撼的。从看问题的视角来说,除了对二元二次方程x^2+y ^2=1表示圆陌生外(在耐心引导下,部分学生还是能够感受到),其他一元一次、二元一次不等式的几何意义(表示平面区域)能够自主总结出来,从而从数、式、形三个层面,给他们提供了如何看待函数、方程、不等式的全方位视角。
2.从思考问题的方法来看,引申、转化、化归、类比、对应、整体、统计思想这些方法的综合运用,对培养和发展学生分析问题、解决问题的能力,本问题也是难得的教学素材。
3.还有对统计思想、统计方法的渗透。在这个问题中,骰子落在弓形区域的概率P(弓形)是可以计算的,这个概率为(π-2)/4≈0.2854,它与圆周率有关,因而可以利用试验所得(骰子落在弓形区域的)频率来代替概率,从而测得圆周率PI的值(PI=4 P(弓形)+2),这种“计算”圆周率的方法,对初中学段的学生来说,简直不可思议!是万万想不到的。与祖冲之割圆术计算圆周率,从思想方法到技术存在巨大反差,对学生而言,也是突破传统思维,发展创新思维的鲜活案例。这种试验方法统计学上,称之为蒙特卡罗方法。它被广泛运用于科学研究、军事、金融、公用事业等诸多领域。
关注“中考数学当百荟”,感谢您的点赞,转发!点击“了解更多”
,





