6个相连的正方形组成的平面图形,经折叠能否围成正方体问题,是经常会考的问题,在考试中常见于选择题、判断题。这种题有利于培养学生的空间观念和实践、探索能力。一般情况解决这类问题有两种方法:一是动手操作来解决,二是通过空间想象进行确定。
下面给大家带来更为简单有效的判断方法,希望在以后遇到这样的问题时,能够快速准确地解答。
1、“141型”。中间一行4个作侧面,上下两个各作为上下底面, 共有6种基本图形。

2、“132型”。中间3个作侧面,共3种基本图形。
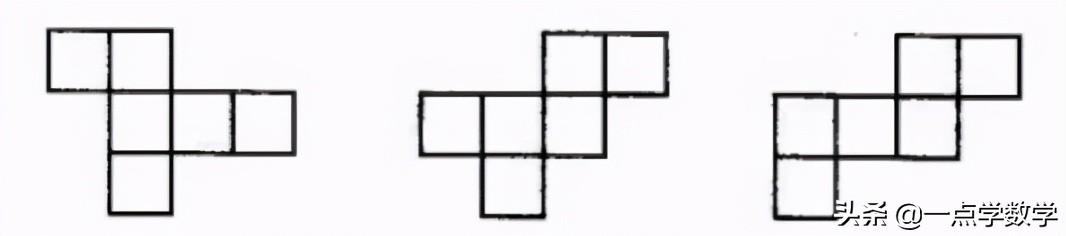
3、“222型”。两行只能有1个正方形相连。

4、“33型”。两行只能有1个正方形相连。

注意:不能出现田字形、凹字形和7字形。

正方体展开图口诀
正方体展有规律,十一种类看仔细;
中间四个 成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四,田七和凹要放弃;
相间之端是对面,间二拐角面相邻。
希望同学们掌握好方法,快速准确地解答相应的问题。注重总结规律,掌握学习方法,祝大家学有所成。
,