大学物理电场学里面有个高斯定理,讲的是静电场的电场特性,定理是这样描述的:静电场中任意封闭曲面的电场通量与曲面所包围的电荷的代数和成正比,与曲面的形状无关,与曲面内电荷的分布无关,与曲面外的电荷无关,这里的电场通量以曲面外侧为正方向,简单来说,就是穿出封闭曲面的电场线数量减穿入曲面的电场线数量就是电场通量,如果封闭曲面内无电荷,那么电场通量就是0,高斯定理在静电场分析中具有重要作用。

高斯画像
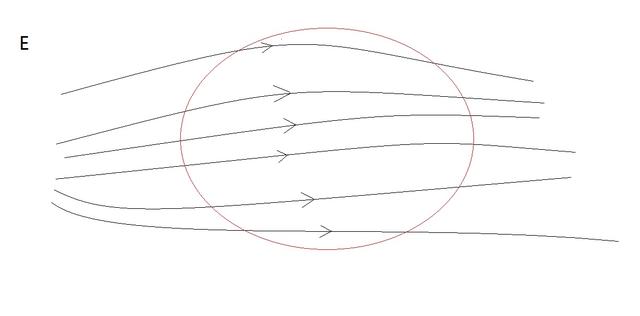
高斯定理图片描述
上图画出来一静电场中的一封闭曲面,黑线为电场线,红线为封闭曲面,可以看到,当封闭曲面内无电荷时,只要穿入曲面的电场线都会穿出曲面,因此电场通量为0。这里我用数学的方式来推导高斯定理,涉及到高等数学的高斯公式,考研的同学不要错过哦,这是考研数学的一个重要应用。下面我来慢慢分析。

单连通区域
这里要讲什么叫单连通区域,意思是空间中一封闭曲面包围的区域完全是实心的,不存在任何空洞,讲高斯公式会用到单连通区域。高斯公式是这样描述的:一空间区域Ω由分块光滑封闭曲面所围成,函数P(x,y,z),Q(x,y,z),R(x,y,z)在Ω内有连续一阶偏导数,意思就是单连通区域,以曲面外侧为正方向,那么高斯公式如下图所示:

高斯公式
高斯公式将曲面积分转换为简单三重积分,简化来计算过程,假如空间区域不是单连通区域,而有空洞,那么称之为复连通区域,如图,

复连通区域
那么此时空间区域Ω由外面的曲面和内部的曲面包围而成,外面的曲面取外侧为正方向,里面的曲面取内侧为正方向,设外面的曲面为S,里面的曲面为S1,S2……Sn,那么复连通区域的高斯公式如下:

复连通区域高斯公式
好了,高斯定理讲了这么多,大家觉得还是很抽象吧,不好理解,没错,光是看这些数学的语言确实很难理解,但是接下里我用高斯公式推导高斯定理,大家就会比较容易理解了。高斯定理的推导先从点电荷入手,设空间中一个电荷量为q的点电荷,如图所示:

点电荷电场
以点电荷为原点建立空间坐标系,根据点电荷电场强度公式E=Kq/r,可以得到空间中(x,y,z)坐标处的电场强度:

这里的i,j,k分别是x,y,z方向的单位向量,在点电荷电场中,我们要求任意包围电荷封闭曲面S1的电场通量,S1包围的区域并非单连通区域,因为在原点处电场强度无定义,此时构造一个足够小的曲面S2,它是以原点为球心的球面,半径r,在S1内部,在此时S1与S2之间的区域就是单连通区域,命名为Ω,那么:


通过上面的推导过程,我们可以得到,包围点电荷的闭合曲面电场通量为4πKq,那么同样当点电荷在曲面外面时可以很容易推出电场通量为0。那么如何推导到一般的情况呢,如果空间的电荷不是点电荷,那怎么办呢?这时,可以采用线性叠加法,将一般的电荷看成很多的点电荷的集合,分别处理,然后将结果叠加。假设空间中有一分块光滑封闭曲面S,里面有n个点电荷,电荷分别为q1,q2....qn,曲面外有m个点电荷,电荷分别为q(n 1)...q(n m),假设有个点电荷为q(a),它在空间产生的电场强度为

由于电场可以线性叠加,所以空间中(x,y,z)处的电场强度为:

所以闭合曲面的电场通量为:

好了,高斯定理已经完全推导出了,所以说,微积分是数学中非常重要的内容,我们现实当中无处不存在数学,喜欢大家都能喜欢上数学。
,




