大楼阻尼器的摆动
上图为台湾101大楼内阻尼器。因为高空强风及台风吹拂造成的摇晃.大楼内设置了“调质阻尼器”,就是在88至92楼挂置一个重达660公吨的巨大钢球,利用摆动来减缓建筑物的晃动幅度
1.简谐振动的运动参量及特征
简谐振动是指系统的运动参量(位移、速度、加速度)按照时间的正弦或余弦函数规律变化的振动,是最简单而又最重要的一种周期振动,如使用余弦函数表达,则简谐振动的位移数学表达式为:

式中的振幅和初相位均由初始条件确定。对位移关于时间求一阶导数和二阶导数,分别得到简谐振动的速度和加速度表达式:

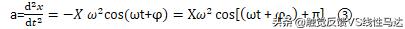
比较以上三式,不难看出简谐振动有以下运动学特征:
(1)简谐振动的速度、加速度、位移也是简谐函数,且简谐函数具有相同的频率;
(2)速度 的相位较位移的相位超前π/2,加速度相位较位移相位超前π;
(3)加速度与位移恒成正比而方向相反,比例系数为圆频率的平方。
简谐运动的位移、速度、加速度时程曲线如下图:

2.简谐振动的矢量表示法
简谐振动可以用旋转的矢量在坐标上的投影来表示,如下图,矢量以等角度逆时针旋转,其模量为A;矢量起始位置与水平周夹角为,任意时刻与水平周夹角为ωt 。此时,旋转矢量在坐标上的投影为简谐函数,如在纵坐标投影为:

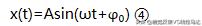
而水平坐标投影为:

与简谐振动方程①比较可见,
旋转矢量的模A正是简谐振动的振幅X,
旋转矢量的角速度是简谐振动的圆频率ω,
旋转矢量与水平轴的夹角是简谐振动的相位角



3.简谐振动的复数表示方法
简谐振动也可以用复数表示,


Z=A(cosθ isinθ) ⑥
可见,复矢量的虚部与实部均为简谐函数,即




根据欧拉公式

简谐振动可用复数表示为


为方便起见,在振动分析中通常将式⑧中的虚部或实部符号省略,这样简谐振动的复数表达式可以写成:

将幅角表达式代入,变为


复变函数以指数形式运算,通常比较简便。假设已知两个复变函数为:

则这两个复变函数的乘积、商和乘方法则如下:

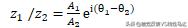

简谐振动若采用复数指数的表达式,通常会给分析运算带来极大的方便。
,