一、抽屉原理“任意367个人中,必有生日相同的人。”“从任意5双手套中任取6只,其中至少有2只恰为一双手套。”“从数1,2,...,10中任取6个数,其中至少有2个数为奇偶性不同。”这里用到的是抽屉原理,抽屉原理的内容可以用形象的语言表述为:“把m个东西任意分放进n个空抽屉里(m>n),那么一定有一个抽屉中放进了至少2个东西。”在上面的第一个结论中,由于一年最多有366天,因此在367人中至少有2人出生在同月同日。这相当于把367个东西放入366个抽屉,至少有2个东西在同一抽屉里。在第二个结论中,不妨想象将5双手套分别编号,即号码为1,2,...,5的手套各有两只,同号的两只是一双。任取6只手套,它们的编号至多有5种,因此其中至少有两只的号码相同。这相当于把6个东西放入5个抽屉,至少有2个东西在同一抽屉里。
利用上述原理容易证明:“任意7个整数中,至少有3个数的两两之差是3的倍数。”因为任一整数除以3时余数只有0、1、2三种可能,所以7个整数中至少有3个数除以3所得余数相同,即它们两两之差是3的倍数。如果问题所讨论的对象有无限多个,抽屉原理还有另一种表述:“把无限多个东西任意分放进n个空抽屉(n是自然数),那么一定有一个抽屉中放进了无限多个东西。”抽屉原理的内容简明朴素,易于接受,它在数学问题中有重要的作用。许多有关存在性的证明都可用它来解决。
二、涨跌停现象
假设你有10万元:
第一种情况:第一天涨停后是11万元,第二天跌停后剩下9.9万元。
第二种情况:第一天跌停后是9万元,第二天涨停后还是9.9万元。
三、补仓或定投现象
假设一个基金净值10元的时候,你买入了1万元。第二个月,基金净值跌到5元的时候,你又买了1万元。
请问:你的持仓成本是多少? A.7.5元 B.6.67元
正确答案:持仓成本是6.67元。
这就是基金定投的魅力,可以让你的持仓成本大幅降低。
四、蜜蜂蜂房
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成。组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料。蜂房的巢壁厚0.073毫米,误差极小。
五、丹顶鹤总是成群结队迁飞,而且排成“人”字形。
“人”字形的角度是110度。更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!
六、冬天,猫睡觉时总是把身体抱成一个球形
这其间也有数学,因为球形使身体的表面积最小,从而散发的热量也最少。
七、保本的资产组合
以下两种投资产品:

假设你有100万元,你投资80万到资产A,投资20万到资产B。
这样你就做出了一个保本的投资组合:最差收益为零,最佳收益为12%。
八、一个带有赌博性质的游戏
主事者将4种不同颜色的球,红、黄、蓝、白每样5个,总共20个,全部放进箱子里,参与者从里面任意摸出10个球。如果4种颜色的组合是5500,就能得到一台莱卡照相机;如果是5410,就送你一条中华烟;但有两个组合是你反过来要给他钱的:一个是3322,一个是4321。
结果玩游戏的人到那儿一抓,经常是3322或4321。这是一道非常容易计算的数学题。西安电子科技大学校长梁昌洪是位数学家,他在学校里组织了几百个学生测试,又在电脑上算,结果都一样:3322和4321所占的比率最高,接近30%;而5500呢,只占十几万分之一。
九、收益率现象
如果你用10万元买了一只股票,涨了100%后是20万;但要再跌50%,就又回到10万元了。要知道,跌50%可比涨100%简单多了。
十、零与无穷大的迷思
“0”也是我感兴趣的数字。我觉得“0”从哲学上说,就是中国人所说的“无”。万物生于有、有生于无,所以无是本源。无当然是本源,因为我们每一个人都生于无。在我们被母亲怀胎之前,我们就是无。
中国人在这个“无”字上是很下功夫的。老子主张无为、无欲,“为学日益,为道日损,损之又损,以至于无为。无为而无不为。”
为什么要“无为无不为”呢?因为有生于无,无又不是都有。所以中国古人又说,无非有,无是没有;无非无,无也不是永远无;无因为能够变成有,所以无非非无,无不是把无给否定了,无本身是不否定无的。无为什么能够变成有呢?因为有了无穷大的帮忙,无和无穷大结合起来,就有可能产生出“有”来。
0和无穷大之间,有和无之间,形成了各种悖论。数学悖论里最基本的问题就是,如果你承认有,那0也是一种有的方式。如果0变成了有的方式,那就太受鼓舞了。

十一、三角形稳定性的应用
看下面我们生活中常见的这些物品了吗,为什么某一部分都做成三角形的?是因为利用了三角形具有稳定性的特点。就像衣架,挂上衣服,衣架也不会变形的。

而单位的推拉门中的连接图形都是四边形,想想如果做成三角形的,会怎么样?这门就推拉不开啦。

十二、从单位到哪家菜市场买菜再回家最近?
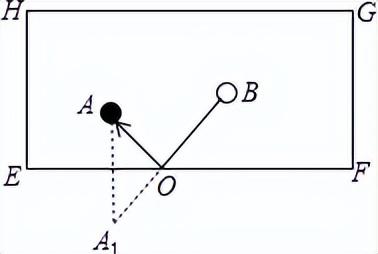
假设A、B两点是你的单位和家,每天下班从超市买菜回家。如果马路上有很多家超市,你从哪家超市买菜,能使得你少跑路呢?

这就是数学中对称性的简单应用,做A关于马路的对称点A1,连接A1和B与马路的交点,对,就到这个位置的超市去买吧,这样你从单位到超市加上再回家的路程和最短。
十三、台球桌上的小知识
大家都喜欢打台球,是一项非常好的娱乐活动。台球里的数学知识和规律有很多。

上面讲到的那个对称性的知识还可以用在打台球上。比如你的白球放在A点,而你要击中的目标球在B处,你要将白球击中边框后再击中目标球,那么应该击打那条边框的哪个点呢?就是下面这张示范图!当然,台球里的数学、物理知识非常多,和击打角度、力度等都有关系,这儿仅仅讲简单一例。
十四、国旗中的数学规律
国旗是一个国家的象征,神圣而庄严。大家都知道国旗是长方形的,这个长方形是随便画出的吗?不是,是黄金矩形。也就是宽与长的比是黄金分割比,大约是0.618。而且不仅是我国国旗,每个国家的国旗都是黄金矩形。这样的矩形图案让我们看起来更舒适,更庄严。

不仅如此,再来看那些五角星,也都符合黄金分割。

(1)C、E两点就是线段AB的两个黄金分割点。
(2)三角形DEC是黄金三角形。也就是底与腰的比是黄金分割比。
(3)三角形ABF也是黄金三角形,腰与底的比是黄金分割比。
是不是很神奇,达芬奇就对黄金分割有着近乎痴迷的崇拜,他的很多艺术作品里充满了黄金分割。
十五、黄金分割在生活中大量存在
(1)很多艺术作品,大量融入了黄金分割,使得构图、视觉效果非常具有美感。

蒙娜丽莎的整个人体结构、脸部结构都符合黄金分割比,所以我们看起来觉得柔美、和谐,有一种特有的美感。还有断臂维纳斯、阿波罗神像等等。

古希腊帕提依神庙里的每个图案都是按黄金分割比严格构图的,给人一种非常庄严、雄伟、圣神的感觉。还有凯旋门、巴黎圣母院、埃菲尔铁塔等等。
(2)自然界中的黄金分割现象也比比皆是。
*我们人体正常温度大约37度左右,我们感到最舒适的温度是23度,这个温度大约就是37度的0.618。
*植物界也有采用黄金分割的地方,如果从一棵嫩枝的顶端向下看,就会看到叶子是按照黄金分割的规律排列着的.
*地球的“黄金分割线”是北纬30 度:北纬30度一带,有地球最高的山峰——珠穆朗玛峰;有地球最深 的海沟——西太平洋马里亚纳海沟;还有百慕大三角区……
*就连音乐中也有黄金比例,琴弦的频率与和谐的音程有固定的比例 ,毕达哥拉斯学派更首次把这种美妙的 音乐称为“和谐”。

*就连报幕员报幕,都不是站在舞台最中央,而是大约三分之一处,黄金分割的位置,看起来舒适和谐,大家在拍照片的时候也可以用一下这个规律啊!
十六、中的数学
大家都知道中是小概率事件。完全靠运气。但是在美国史上有这么一次有趣的小插曲。
2004年秋天,麻省设计了一款新。他规定如果一周之内没有人获取大奖,并且大奖基金超过200万美元的时候,奖金就会向低奖此分配,增加低等奖的获奖金额。这种机制导致花2美元买一张,而期望值高达5.53美元,这简直是意想不到的天大好事。
首先发现这个空子的是麻省理工的学生们,他们组团购买了1000张,获得了三倍的收获。以后这简直就成了他们的副业。直到2012年,麻生发现了这个空子,取消了这款,但此时麻生理工学院的学生们已经获得了350万美金的奖金。
十七、银行理财中的数学
现在很多人买银行理财和大额存单。我们看到有些银行的理财利率相对较高,3个月的存钱利率4.5%,而大额存单3年的利率最高4.18%。这样算下来,以20万来算3年相差2000元左右。
但是,这期间没考虑3个月理财中间有空档期、募集期、利率预期下调等因素,算下来不如大额存单合算呢!
其实,生活中的数学规律举不胜举,我仅仅举其中简单几例。数学是我们社会生活、科学的基础,渗透在我们的方方面面,数学的作用大着呢!
扩展资料:
数学(mathematics或maths,来自希腊语,“máthēma”;经常被缩写为“math”),是研究数量、结构、变化、空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种。数学家和哲学家对数学的确切范围和定义有一系列的看法。
而在人类历史发展和社会生活中,数学也发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具。
,




