工业机器人的机械结构一般都存在几何误差,如连杆长度偏差、关节距离偏差、关节角度偏差、零位校准偏差等,这些都可以算是工业机器人的几何误差。由于几何误差的存在,工业机器人都存在绝对定位精度过低的通病,虽然重复定位精度可能很高。
由于几何误差的存在,这就需要我们对工业机械手进行校准。工业机器人的标准的DH运动学算法中每个关节处只有四个参数,即α、d、a、θ,其含义可参考相关的机器人学教程。工业机械手几何误差的校准需要用到雅可比矩阵,我们需要根据DH运动学算法建立机械手末端工具位姿(X、Y、Z、U、V、W)与连杆参数(α、d、a、θ)的微分关系。微分校准算法假设以下条件成立,即:工业机械手模型中某个关节处的连杆参数(α、d、a、θ)的微小的变化只会导致其它参数微小的变化(而不是显著的很大的变化,即微分变化)。然而当机械手的两个邻近的轴平行(或接近平行)时,如果采用DH运动学算法,这个假设就不能成立。这是因为,如果两个邻近的关节轴(Zi和Zj)如果处于理想的平行状态的话,坐标系i的坐标轴Xi可以选择在沿着坐标轴Zi轴的任何地方(DH运动学模型中规定的坐标轴Xi的定义方法)。当两个邻近的平行轴之间出现细微的偏差时,即它们不再平行,根据DH运动学模型建立方法,如果两个邻近的关节轴不平行,选择两个关节轴的公垂线方向作为坐标系j的Xj轴的方向,公垂线与Zj轴的交点为坐标系j的原点。出现偏差后的坐标系j的原点与原来处于平行状态时选择的坐标系j的原点之间有可能会出现很大的偏差(处于平行状态时坐标系j的原点可以选择在Zj轴上的任意位置),这就使得一个关节轴参数的细微变化而引起了其它参数的巨大变化,这与以上提出的假设条件相悖。我们所常见的工业六轴关节机器人,其第二和第三轴的理想模型都是处于平行状态的,因此标准的DH运动学算法不适合于进行机器人的误差校准。这就需要对DH运动学模型进行修正。因此国外提出了DH运动学模型的改进版,即修正的DH运动学模型。

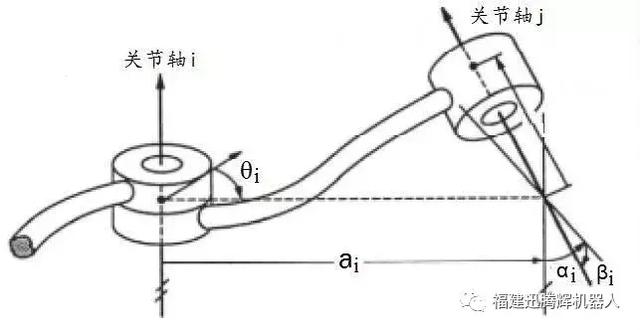
在修正的DH运动学模型中,引入了一个新的关节变量,即β,它表示绕Y轴旋转β角度。在工业机器人运动学建模中,对于邻近的关节轴相互平行轴的情况,我们采用修正的DH表示法(用修正的DH表示法建模),引入关节变量β,而舍弃标准DH表示法中的关节变量d,这样修正的DH表示法中的关节变量分别为:θ、a、α、β,变量个数依旧为四个;对于邻近的关节轴相互垂直的情况,依旧采用标准的DH表示法建模,其关节变量分别为:θ、d、a、α。
当采用修正的DH表示法运动学模型时,坐标变换的顺序依次为:
1.绕Zi轴旋转θj,使得Xi和Xj互相平行;
2.沿Xi轴平移aj的距离,使得Xi与Xj原点重合;
3.将Zi轴绕Xj轴旋转αj;
4.将Zi轴绕Yj轴旋转βj。
通过以上四个变换步骤完成从坐标系i到j的变换。
变换矩阵为:
T=Rot(Z,θj)×Trans(aj,0,0)×Rot(X,αj)×Rot(Y,βj)
当运动学模型为理想模型时,即两相邻关节绝对平行时,βj=0。
以上所述即为修正的DH表示法对工业机器人进行建模的方法。