
详细介绍高斯分布及其与均值、标准差、方差的关系
高斯分布是统计中最重要的概率分布,在机器学习中也很重要。因为很多自然现象,比如人口的身高,血压,鞋子的尺码,教育指标,考试成绩,还有很多更重要的自然因素都遵循高斯分布。
我相信,你听说过这个词,在某种程度上也知道它。如果没有,也不要担心。这篇文章将会解释清楚。我在Coursera的Andrew Ng教授的机器学习课程中发现了一些令人惊叹的视觉效果。他知道如何将一个主题分解成小块,使它更容易解释。
他使用了一些可视化方法,让人们很容易理解高斯分布及其与相关参数(如均值、标准差和方差)的关系。
在这篇文章中,我从他的课程中截取了一些图像,并在这里用它来详细解释高斯分布。
高斯分布高斯分布是正态分布的同义词。它们是一样的东西。假设,S是一组随机值,其概率分布如下图所示。
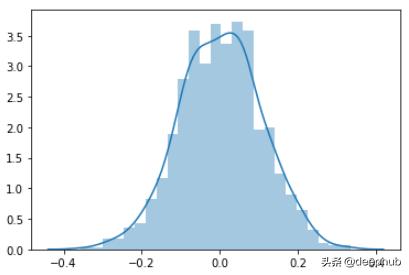
这是一个钟形曲线。如果一个概率分布图像上面那样形成一个钟形曲线,并且该样本的均值和中位数相同,则该分布称为正态分布或高斯分布。
高斯分布由两个参数:
a.平均数
b.方差
所以,高斯密度在mu或均值处是最高的,离均值越远,高斯密度就越低。
这是高斯分布的公式:

方程左边是x的概率参数是和的平方。这是钟形曲线的公式其中平方称为方差。
高斯分布与平均值和标准差有什么关系在这一节中,我将展示一些图片,让你们清楚地了解参数和与钟形曲线的关系。我将展示三幅图在这三幅图中mu固定在0处而sigma不同。
注意曲线的形状和范围是如何随不同的sigma变化的。

这是一组随机数的概率分布mu = 0,而sigma = 1。
在这幅图中,mu是0,这意味着最大的概率密度是0,sigma是1。表示曲线的宽度是1。
注意,曲线的高度大约是0.5,范围是-4到4(看x轴)。方差的平方是1。

这是另一组随机数0,0.5。
因为mu是0,就像之前的图一样最大的概率密度是0,sigma是0.5。曲线的宽度是0.5。方差的平方变成0.25。
由于曲线的宽度是前一条曲线的一半,因此高度加倍。范围改变为-2到2 (x轴),这是前一张图片的一半。

在这幅图中,sigma= 2 mu= 0。
将其与图1比较,其中sigma为1。这一次,高度变成了图1的一半,宽度随着变成两倍。
方差平方是4,比图1大4倍。x轴的范围是-8到8。

此示例与前三个示例略有不同。
这里,我们把mu改为3 sigma = 0.5,如图2所示。因此,曲线的形状与图2完全相同,只是中心移动到了3。现在最大的密度是3。
上面的四条曲线用不同的参数改变形状但曲线的面积保持不变。
概率分布的一个重要性质是,曲线下的面积积分为1。
参数计算假设我们有一系列数据。如何计算mu(均值)和标准差?
mu的计算很简单。这只是平均数。把所有数据的总和除以数据的总数。

这里,xi是数据集中的单个值,m是数据的总数。
方差公式为:

标准差就是方差的平方根。
多元高斯分布假设有多组数据,我们需要多元高斯分布。假设我们有两组数据;x1和x2。
单独建模p(x1)和p(x2)对于理解两个数据集的组合效果可能不是一个好主意。在这种情况下,您可能希望将数据集和模型仅结合在一起建立p(x)。
这是计算多元高斯分布概率的公式,

在本节中,我们将看到多元高斯分布的可视化表示,以及曲线的形状如何随mu、sigma以及变量之间的相关性而变化。
从标准正态分布开始

该图表示多元高斯分布的概率分布,其中x1和x2的mu都为零。
请不要被这里的求和符号搞糊涂了。这是一个单位矩阵,其中对角线上的1是x1和x2的sigma。而非对角线上的零表示x1和x2之间的相关性。在这个例子中x1和x2是不相关的。
这里的图片很简单。在x1和x2方向上,当mu为0时,最大的概率密度为0。
中间的深红色区域是概率密度最高的区域。在浅红色、黄色、绿色和青色区域,概率密度继续降低。深蓝色区域是最低的。
改变标准差

现在,让我们看看如果sigma变小一点会发生什么。x1 x2的sigma都是0.6。
正如我之前提到的,曲线下的面积要积分为1。标准差减小时,曲线范围减小。同时,曲线的高度变高,以调整区域。

相反,当sigma越大,范围就越大。所以曲线的高度变低了。
看看图6,曲线和范围的高度变化几乎与我之前在单变量高斯分布中显示的图相似。
x1和x2的值并不总是相同的。我们来看看这样的例子。

在图7中,x1的sigma = 0.6, x2的sigma = 1。
x1的范围变小了,因为标准差变小了。

在图8中,它与前一张图相反。
x1的sigma是x2的两倍。
这次x1有更大的范围。
改变变量之间的相关因素

这是一个完全不同的场景。在图9中,非对角线值不再是零。而是0.5。它表明x1和x2的相关系数为0.5。
x1和x2的范围是一起增长的因为它们是正相关的。
当x1大时,x2也大当x1小时,x2也小。

在图10中,x1和x2之间的相关性更大,为0.8!
所有的概率都在一个狭窄的区域内。分布也看起来又高又瘦。
在上面所有的图片中,x1和x2之间的相关性要么是正的,要么是零。让我们看一个相关系数为负的例子。

在图11中,x1和x2的相关性为-0.8。
你可以看到概率又在一个小范围内了。但是当x1大,x2小,当x1小,x2大。
最后,我们需要检验不同均值我们来看看mu不同时图像的变化。

在图12中,mu对于x1是0,对于x2是0。5。
看看图片上的范围。对于x2,曲线的中心从0开始移动。
中心位置或最高概率分布点现在应该是0.5。

在图13中,mu对于x1 为1.5,对于x2 mu为-0.5。
x1方向上最高概率点是1.5。同时,对于x2方向,最高概率点为-0.5。
总的来说,整个曲线都在移动。
结论我希望这篇文章对理解高斯分布和它的特征有帮助。我试图展示和解释曲线与不同参数之间的关系。希望,当你在统计或机器学习中使用高斯分布时,会简单得多。
作者:Rashida Nasrin Sucky
deephub翻译组:孟翔杰
,




