关于超穷理论的内容,我分成上中下三部分,第一部分讲“数学历史",第二部分将"无穷大基本概念",第三部分讲“超穷理论”,喜欢的读者朋友们,可以根据自己的喜好选择其阅读内容。
前一篇我们介绍了无穷大的基本概念,还引入一个工具叫“射映”。在这篇文章中,我们将利用这些简单的概念,去了解超穷理论的精髓!
康托尔(Cantor,1845-1918,德国数学家)虽然遭到同行的挤压,但他从未停止自己对数学和真理的追求!他在想,正整数集合和平方数集合可以一一对应,那么他们的个数某种程度上应该是相等的。
康托尔把集合的个数称作“基数”(有的也称“势”),有限集合基数叫做有穷基数,无限集合的基数叫做超穷基数。
另外,他把和自然数可以一一对应的所有集合叫做可数集合,可数集合的基数用b表示!(可数并不是说有限,实质上它的基数还是无穷)然后康托尔以此为基础,创造了一系列关于基数的运算法则。
然后他立马遇到了第一个难题,有理数的基数能和自然数一一对应吗?
康托尔对角线发展
按照图纸箭头走法,我们将“逐一”取遍所有正有理数(这里我们无需弄复杂把负数拿出了,因为后面我们会知道:正有理数和有理数都是可数的),也就有理数是可以和自然数一一对应。
怎么样!这个结果你没想到吧,第一次想到这个对应关系的绝对是天才!
好了,有理数的问题解决了,下一步,康托尔自然要去研究实数,那么实数集是可数集合吗???(注:这时候,第一次数学危机“无理数危机”持续了2000多年,刚于1872年被彻底解决)

第一次数学危机
这个问题确实不容易,康托尔试了各种办法,都无法找到一种对应方式,把自然数射映到实数上,以他那非凡的天赋,他必定会想到:或许实数根本就是不可数的!
这就是康托尔超穷理论的第二个重大发现——实数集是不可数的!
不可数代表实数无法一一射映于自然数,实数集的基数用c表示,这个发现预言了无理数的存在,而且无理数远远要比有理数“稠密”!
这下可把数学界炸开了锅,有接踵而至的表扬,也有狂风暴雨般的批判和攻击,在1891年,康托尔又证明了超穷理论中一个重要定理——康托尔定理!
其内容意思是:所有集合的子集组成的集合,其基数(y)一定大于原集合的基数(x),并满足y=2^x!
因为集合每个元素的子集就是对每个元素选择留与不留,所以是已2为底。
这个定理非常强,小至空集,大致无穷基数的集合都成立,并从严格的数学逻辑推导出:实数集的基数就是正整数集合的所有子集的基数,换句话说c=2^b(如果你还没忘记b和c表示什么的话),同样我们可以得到“实数集合的所有子集集合”的基数比“实数集合”的基数大,一步步下去,我们就得到了不同的无穷基数d,e,f……
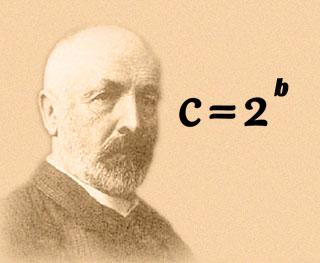
康托尔
其中可数基数(b)叫做阿列夫零,记作ℵ₀;
下一个(c)叫ℵ₁ ;
再下一个(d)是ℵ2;
那么根据康托尔定理就会有:ℵ₁=2^ℵ₀,ℵ2=2^ℵ₁……

阿列夫零
其中ℵ₁ 又称连续统的势,每个阿列夫数都对应于某个无穷大的势,注意,前面我们说无穷大是不能比较大小的,所以我们换了个概念——“势”,换句话说,其实就是无穷大是有区别的,但是理解起来并不容易。
超穷理论里面,有个很大的问题,就是ℵ₀和ℵ₁ 之间有其他的阿列夫数吗?康托尔觉得是没有的,这叫“连续统假设”,希尔伯特把这个问题作为他的二十三数学难题之首,排在了黎曼猜想和哥德巴赫猜想之前,足以看出其重要性和难度之大,不过后来数学家证明,这个假设是“不可判定的”,也就是说不能在其体系内证明也不能证伪,尤如欧式几何的第五公设的情况一样,那里会是另外一片数学领域。

第五公设
对于无穷大的处理,自从康托尔提出超穷理论后不再神秘,尤其是在物理学中,也出现了很多无穷大,这对物理学家来说简直就是噩梦,历经多年后,物理学家从找到了处理无穷大的办法——重整化,比如前面我提到的级数1 2 3 4 ……-1/12出现在弦理论中,就是利用了重整化的思想。

全体自然数之和
对于无穷大,数学家希尔伯特曾经提出一个经典的例子,叫希尔伯特旅馆:
我们设想有一家旅馆,内设有限个房间,而所有的房间都已客满。这时来了一位新客想订个房间,“对不起”,旅馆主人说,“所有的房间都住满了。”

希尔伯特旅馆
现在再设想另一家旅馆,内设无限个房间,所有的房间也都满了。
第一天:来了一位新客,想订个房间。“不成问题!”旅馆主人说。接着他就把1号房间的旅客移到2号房间,2号房间的旅客移到3号房间,3号房间的旅客移到4号房间等等,这样继续移下去。这样一来,新客就被安排住进了已被腾空的1号房间。
第二天:又来了无穷多位要求订房间的客人。“好的,先生们,请等一会儿。”旅馆主人说。
于是他把1号房间的旅客移到2号房间,2号房间的旅客移到4号房间,3号房间的旅客移到6号房间,如此等等,这样继续下去。现在,所有的单号房间都腾出来了,新来的无穷多位客人也都可以住进去,问题解决了!
第三天:又来了无穷多个旅行团,每个旅行团有无穷多个旅客,只见这个老板不慌不忙,让原来的旅客1号房间客人搬到2号,2号房间客人搬到4号……,k号房间客人搬到2k号。这样,1号,3号,5号……所有奇数房间就都空出来了,然后:
让1号旅行团到3号,3*2号,3*3号,3*4号,…,3k号。
让2号旅行团到5号,5*2号,5*3号,5*4号,…,5k号。
让3号旅行团到7号,7*2号,7*3号,7*4号,…,7k号。
让4号旅行团到11号,11*2号,11*3号,11*4号,…,11k号。
将所有奇素数排成一列,也是一个可列无穷集合,然后让
1号旅行团到第1个素数的k次幂房间;
2号旅行团到第2个素数的k次幂房间;
3号旅行团到第3个素数的k次幂房间…这样不仅安排下了所有旅客,而且空出了1,15,21,33,35……这些不能表示为奇素数的k次幂的房间。
第四天:所有入驻的客人,每个客人都来了无数个亲戚,请问:旅客老板还有办法把这些客人的所有亲戚安排到旅馆中吗?
这个问题,就留给读者朋友们思考吧!如果你理解了超穷理论的概念,那么这个问题就很容易回答了!
好啦!以上所有内容就介绍到这里,有兴趣的读者朋友们,可以自行去了解更多关于超穷数理论的知识,当然也可以关注我们,给我们留言。
,




