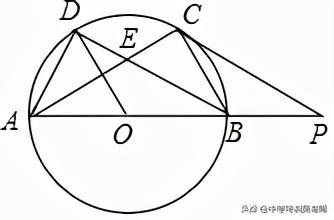
1.(12分)如图,AB是⊙O的直径,弦 AC与 BD交于点 E,且 AC=BD,连接 AD,BC.
(1)求证:△ADB≌△BCA;
(2)若 OD⊥AC,AB=4,求弦 AC的长;
(3)在(2)的条件下,延长 AB支点 P,使 BP=2,连接 PC.求证:PC是⊙O的切线.
2.(12分)如图,已知 AB是⊙O的直径,点 P是⊙O上一点,连接 OP,点 A关于 OP的
对称点 C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过点 C座⊙O的切线 CD,交 AP的延长线于点 D.如果∠D=90°,DP=1,求
⊙O的直径.

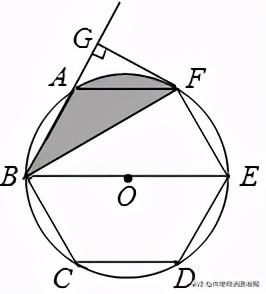
3.(12分)如图,正六边形 ABCDEF内接于⊙O,BE是⊙O的直径,连接 BF,延长 BA,
过 F作 FG⊥BA,垂足为 G.
(1)求证:FG是⊙O的切线;
(2)已知 FG=2 ,求图中阴影部分的面积.
4.(12分)如图,在△ABC中,AB=AC,以 AB为直径的⊙O与边 BC,AC分别交于 D,
E两点,过点 D作 DH⊥AC于点 H.
(1)判断 DH与⊙O的位置关系,并说明理由;
(2)求证:H为 CE的中点;
(3)若 BC=10,cos∠C=√5/5 ,求 AE的长.

5.(12分)如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦 AD,BC相交于
点 E.
(1)求证: = ;
(2)若 CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点 C作⊙O的切线,交 BA的延长线于点 P,过点 P作 PQ∥
CB交⊙O于 F,Q两点(点 F在线段 PQ上),求 PQ的长.

6.(12分)如图,在菱形 ABCD中,连接 BD、AC交叉点 O,过点 O作 OH⊥BC于点 H,
一点 O为圆心,OH为半径的半圆角 AC于点 M.
①求证:DC是⊙O的切线.
②若 AC=4MC且 AC=8,求图中阴影部分的面积.
③在②的条件下,P是线段 BD上的一动点,当 PD为和值时,PH PM的值最小,并求
出最小值.

7.(12分)已知:如图,AB、AC是⊙O的两条弦,且 AB=AC,D是 AO延长线上一点,
联结 BD并延长交⊙O于点 E,连接 CD并延长交⊙O于点 F.
(1)求证:BD=CD;
(2)如果 AB2=AO•AD,求证:四边形 ABDC是菱形.

8.(12分)如图 1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点 C作∠BCD=∠
ACB交⊙O于点 D,连接 AD交 BC于点 E,延长 DC支点 F,使 CF=AC,连接 AF.
(1)求证:ED=EC;
(2)求证:AF是⊙O的切线;
(3)如图 2,热点 G是△ACD的内心,BC•BE=25,求 BG的长.

9.(12分)如图,已知锐角三角形 ABC内接于圆 O,OD⊥BC于点 D,连接 OA.
(1)若∠BAC=60°,
①求证:OD= OA.
②当 OA=1时,求△ABC面积的最大值.
(2)点 E在线段 OA上,OE=OD,连接 DE,设∠ABC=m∠OED,∠ACB=n∠OED
(m,n是正数),若∠ABC<∠ACB,求证:m﹣n 2=0.

10.(14分)如图 1,⊙O经过等边△ABC的顶点 A,C(圆心 O在△ABC内),分别与 AB,
CB的延长线交于点 D,E,连结 DE,BF⊥EC交 AE于点 F.
(1)求证:BD=BE.
(2)当 AF:EF=3:2,AC=6时,求 AE的长.
(3)设 =x,tan∠DAE=y.
①求 y关于 x的函数表达式;
②如图 2,连结 OF,OB,若△AEC的面积是△OFB面积的 10倍,求 y的值.

11.(12分)如图,AB是⊙O的直径,M、D两点在 AB的延长线上,E是⊙C上的点,且
DE2=DB•DA,延长 AE至 F,使得 AE=EF,设 BF=10,cos∠BED= .
(1)求证:△DEB∽△DAE;
(2)求 DA,DE的长;
(3)热点 F在 B、E、M三点确定的圆上,求 MD的长.

12.(10分)如图,抛物线 y=ax2 6ax(a为常数,a>0)与 x轴交于 O,A两点,点 B为
抛物线的顶点,点 D的坐标为(t,0)(﹣3<t<0),连接 BD并延长与过 O,A,B三点
的⊙P相交于点 C.
(1)求点 A的坐标;
(2)过点 C作⊙P的切线 CE交 x轴于点 E.
①如图 1,求证:CE=DE;
②如图 2,连接 AC,BE,BO,当 a= ,∠CAE=∠OBE时,求 ﹣ 的值.
























1.【分析】(1)可证∠ACB=∠ADB=90°,则由 HL定理可证明结论;
(2)可证 AD=BC=DC,则∠AOD=∠ABC=60°,由直角三角形的性质可求出 AC的
长;
(3)可得出 BC=BP=2,∠BCP=30°,连接 OC,可证出∠OCP=90°,则结论得证.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵AB=AB,
∴△ADB≌△BCA(HL);
(2)解:如图,连接 DC,
∵OD⊥AC,
∴ ,
∴AD=DC,
∵△ADB≌△BCA,
∴AD=BC,
∴AD=DC=BC,
∴∠AOD=∠ABC=60°,
∵AB=4,
∴ ;
(3)证明:如图,连接 OC,
∵BC=BP=2
∴∠BCP=∠P,
∵∠ABC=60°,
∴∠BCP=30°,
∵OC=OB,∠ABC=60°,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠OCP=∠OCB ∠BCP=60° 30°=90°,
∴OC⊥PC,
∴PC是⊙O的切线.
【点评】本题是圆的综合题,考查了圆的有关知识,全等三角形的判定和性质,等边三
角形的性质,直角三角形的性质,添加恰当辅助线是本题的关键.
2.【分析】(1)由题意可知 = ,根据同弧所对的圆心角相等得到∠AOP=∠POC=
∠AOC,再根据同弧所对的圆心角和圆周角的关系得出∠ABC= ∠AOC,利用同位
角相等两直线平行,可得出 PO与 BC平行;
(2)由 CD为圆 O的切线,利用切线的性质得到 OC垂直于 CD,有 AD垂直于 CD,利
用平面内垂直于同一条直线的两直线平行得到 OC与 AD平行,根据两直线平行内错角相
等得到∠APO=∠COP,由∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由 OA
=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形 AOP三内角相等,
确定出三角形 AOP为等边三角形,根据等边三角形的内角为 60°得到∠AOP为 60°,
由 OP平行于 BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由 OB
=OC,得到三角形 OBC为等边三角形,可得出∠COB为 60°,利用平角的定义得到∠
POC也为 60°,再加上 OP=OC,可得出三角形 POC为等边三角形,得到内角∠OCP
为 60°,可求出∠PCD为 30°,在直角三角形 PCD中,利用 30°所对的直角边等于斜
边的一半可得出 PD为 PC的一半,而 PC等于圆的半径 OP等于直径 AB的一半,可得
出 PD为 AB的四分之一,即 AB=4PD=4.
【解答】(1)证明:∵A关于 OP的对称点 C恰好落在⊙O上.
∴ =
∴∠AOP=∠COP,
∴∠AOP= ∠AOC,
又∵∠ABC= ∠AOC,
∴∠AOP=∠ABC,
∴PO∥BC;
(2)解:连接 PC,
∵CD为圆 O的切线,
∴OC⊥CD,又 AD⊥CD,
∴OC∥AD,
∴∠APO=∠COP,
∵∠AOP=∠COP,
∴∠APO=∠AOP,
∴OA=AP,
∵OA=OP,
∴△APO为等边三角形,
∴∠AOP=60°,
又∵OP∥BC,
∴∠OBC=∠AOP=60°,又 OC=OB,
∴△BCO为等边三角形,
∴∠COB=60°,
∴∠POC=180°﹣(∠AOP ∠COB)=60°,又 OP=OC,
∴△POC也为等边三角形,
∴∠PCO=60°,PC=OP=OC,
又∵∠OCD=90°,
∴∠PCD=30°,
在 Rt△PCD中,PD= PC,
又∵PC=OP= AB,
∴PD= AB,
∴AB=4PD=4.
【点评】此题考查了切线的性质,等边三角形的判定与性质,含 30°直角三角形的性质,
轴对称的性质,圆周角定理,以及平行线的判定与性质,熟练掌握性质及判定是解本题
的关键.
3.【分析】(1)连接 OF,AO,由 AB=AF=EF,得到 = = ,求得∠ABF=∠AFB
=∠EBF=30°,得到 AB∥OF,求得 OF⊥FG,于是得到结论;
(2)由 = = ,得到∠AOF=60°,得到△AOF是等边三角形,求得∠AFO=60°,
得到 AO=4,根据扇形的面积公式即可得到结论.
【解答】(1)证明:连接 OF,AO,
∵AB=AF=EF,
∴ = = ,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵ = = ,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2 ,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积= = .
【点评】本题考查了正多边形与圆,切线的判定,等边三角形的判定和性质,扇形的面
积的计算,正确的作出辅助线是解题的关键.
4.【分析】(1)连结 OD、AD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰
三角形的性质得 BD=CD,再证明 OD为△ABC的中位线得到 OD∥AC,加上 DH⊥AC,
所以 OD⊥DH,然后根据切线的判定定理可判断 DH为⊙O的切线;
(2)连结 DE,如图,有圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然
后根据等腰三角形的性质得到 CH=EH;
(3)利用余弦的定义,在 Rt△ADC中可计算出 AC=5 ,在 Rt△CDH中可计算出 CH
= ,则 CE=2CH=2 ,
然后计算 AC﹣CE即可得到 AE的长.
【解答】(1)解:DH与⊙O相切.理由如下:
连结 OD、AD,如图,
∵AB为直径,
∴∠ADB=90°,即 AD⊥BC,
∵AB=AC,
∴BD=CD,
而 AO=BO,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DH⊥AC,
∴OD⊥DH,
∴DH为⊙O的切线;
(2)证明:连结 DE,如图,
∵四边形 ABDE为⊙O的内接四边形,
∴∠DEC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠DEC=∠C,
∵DH⊥CE,
∴CH=EH,即 H为 CE的中点;
(3)解:在 Rt△ADC中,CD= BC=5,
∵cosC= = ,
∴AC=5 ,
在 Rt△CDH中,∵cosC= = ,
∴CH= ,
∴CE=2CH=2 ,
∴AE=AC﹣CE=5 ﹣2 =3 .
【点评】本题考查了圆的综合题:熟练掌握圆周角定理、切线的判定定理和等腰三角形的判
定与性质;会利用三角函数的定义解直角三角形.
5.【分析】(1)由等腰三角形的性质和平行线的性质可得∠OBC=∠CBD,即可证 = ;
(2)通过证明△ACE∽△BCA,可得 ,可得 AC=2,由勾股定理可求 AB的长,
即可求⊙O的半径;
( 3)过点 O 作 OH⊥FQ 于点 H,连接 OQ,通过证明△APC∽△CPB,可得
,可求 PA= ,即可求 PO的长,通过证明△PHO∽△BCA,
可求 PH,OH的长,由勾股定理可求 HQ的长,即可求 PQ的长.
【解答】证明:(1)∵OC=OB
∴∠OBC=∠OCB
∵OC∥BD
∴∠OCB=∠CBD
∴∠OBC=∠CBD
∴
(2)连接 AC,
∵CE=1,EB=3,
∴BC=4
∵
∴∠CAD=∠ABC,且∠ACB=∠ACB
∴△ACE∽△BCA
∴
∴AC2=CB•CE=4×1
∴AC=2,
∵AB是直径
∴∠ACB=90°
∴AB= =2
∴⊙O的半径为
(3)如图,过点 O作 OH⊥FQ于点 H,连接 OQ,
∵PC是⊙O切线,
∴∠PCO=90°,且∠ACB=90°
∴∠PCA=∠BCO=∠CBO,且∠CPB=∠CPA
∴△APC∽△CPB
∴
∴PC=2PA,PC2=PA•PB
∴4PA2=PA×(PA 2 )
∴PA=
∴PO=
∵PQ∥BC
∴∠CBA=∠BPQ,且∠PHO=∠ACB=90°
∴△PHO∽△BCA
∴
即
∴PH= ,OH=
∴HQ= =
∴PQ=PH HQ=
【点评】本题考查了切线的性质,圆的有关知识,相似三角形的判定和性质,勾股定理,
求出 PA的长是本题的关键.
6.【分析】①作 OH⊥BC,证明 OH为圆的半径,即可求解;
②利用 S 阴影=S△OCB﹣S 扇形OHM= CH•OH﹣ OH2,即可求解;
③作M关于 BD的对称点N,连接HN交 BD于点 P,PH PM=PH PN=HN,此时 PH PM
最小,即可求解.
【解答】解:①过点 O作 OG⊥CD,垂足为 G,
在菱形 ABCD中,AC是对角线,则 AC平分∠BCD,
∵OH⊥BC,OG⊥CD,
∴OH=OG,
∴OH、OG都为圆的半径,即 DC是⊙O的切线;
②∵AC=4MC且 AC=8,
∴OC=2MC=4,
MC=OM=2,
∴OH=2,
在直角三角形 OHC中,HO= CO,
∴∠OCH=30°,∠COH=60°,
∴HC= ,OB=
S 阴影=S△OCB﹣S 扇形OHM= CO•OB﹣ OH2= ﹣ ;
③作 M关于 BD的对称点 N,连接 HN交 BD于点 P,
∵PM=NP,
∴PH PM=PH PN=HN,此时 PH PM最小,
∵ON=OM=OH,
∠MOH=60°,
∴∠MNH=30°,
∴∠MNH=∠HCM,
∴HN=HC=2 ,
即:PH PM的最小值为 2 ,
在 Rt△NPO中,
OP=ONtan30°= ,
在 Rt△COD中,
OD=OCtan30°= ,
则 PD=OP OD=2 .
【点评】本题为圆的综合运用题,涉及到圆切线的性质及应用、点的对称性、解直角三
角形等知识,其中③,通过点的对称性确定 PH PM最小,是本题的难点和关键.
7.【分析】(1)连接 BC,根据 AB=AC,OB=OA=OC,即可得出 AD垂直平分 BC,根
据线段垂直平分线性质求出即可;
(2)根据相似三角形的性质和判定求出∠ABO=∠ADB=∠BAO,求出 BD=AB,再根
据菱形的判定推出即可.
【解答】证明:(1)如图 1,连接 BC,OB,OC,
∵AB、AC是⊙O的两条弦,且 AB=AC,
∴A在 BC的垂直平分线上,
∵OB=OA=OC,
∴O在 BC的垂直平分线上,
∴AO垂直平分 BC,
∴BD=CD;
(2)如图 2,连接 OB,
∵AB2=AO•AD,
∴ = ,
∵∠BAO=∠DAB,
∴△ABO∽△ADB,
∴∠OBA=∠ADB,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠OAB=∠BDA,
∴AB=BD,
∵AB=AC,BD=CD,
∴AB=AC=BD=CD,
∴四边形 ABDC是菱形.
【点评】本题考查了相似三角形的性质和判定,圆心角、弧、弦之间的关系,线段垂直
平分线的性质,菱形的判定,垂径定理等知识点,能综合运用知识点进行推理是解此题
的关键.
8.【分析】(1)由 AB=AC知∠ABC=∠ACB,结合∠ACB=∠BCD,∠ABC=∠ADC得
∠BCD=∠ADC,从而得证;
(2)连接 OA,由∠CAF=∠CFA知∠ACD=∠CAF ∠CFA=2∠CAF,结合∠ACB=∠
BCD得∠ACD=2∠ACB,∠CAF=∠ACB,据此可知 AF∥BC,从而得 OA⊥AF,从而
得证;
(3)证△ABE∽△CBA得 AB2=BC•BE,据此知 AB=5,连接 AG,得∠BAG=∠BAD
∠DAG,∠BGA=∠GAC ∠ACB,由点 G为内心知∠DAG=∠GAC,结合∠BAD ∠DAG
=∠GAC ∠ACB得∠BAG=∠BGA,从而得出 BG=AB=5.
【解答】解:(1)∵AB=AC,
∴∠ABC=∠ACB,
又∵∠ACB=∠BCD,∠ABC=∠ADC,
∴∠BCD=∠ADC,
∴ED=EC;
(2)如图 1,连接 OA,
∵AB=AC,
∴ = ,
∴OA⊥BC,
∵CA=CF,
∴∠CAF=∠CFA,
∴∠ACD=∠CAF ∠CFA=2∠CAF,
∵∠ACB=∠BCD,
∴∠ACD=2∠ACB,
∴∠CAF=∠ACB,
∴AF∥BC,
∴OA⊥AF,
∴AF为⊙O的切线;
(3)∵∠ABE=∠CBA,∠BAD=∠BCD=∠ACB,
∴△ABE∽△CBA,
∴ = ,
∴AB2=BC•BE,
∴BC•BE=25,
∴AB=5,
如图 2,连接 AG,
∴∠BAG=∠BAD ∠DAG,∠BGA=∠GAC ∠ACB,
∵点 G为内心,
∴∠DAG=∠GAC,
又∵∠BAD ∠DAG=∠GAC ∠ACB,
∴∠BAG=∠BGA,
∴BG=AB=5.
【点评】本题是圆的综合问题,解题的关键是掌握圆心角定理、切线的判定与性质、相
似三角形的判定与性质等知识点.
9.【分析】(1)①连接 OB、OC,则∠BOD= BOC=∠BAC=60°,即可求解;②BC
长度为定值,△ABC面积的最大值,要求 BC边上的高最大,即可求解;
(2)∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣m x﹣n x= ∠BOC=∠DOC,而∠AOD
=∠COD ∠AOC=180°﹣m x﹣n x 2mx=180° m x﹣n x,即可求解.
【解答】解:(1)①连接 OB、OC,
则∠BOD= BOC=∠BAC=60°,
∴∠OBC=30°,
∴OD= OB= OA;
②∵BC长度为定值,
∴△ABC面积的最大值,要求 BC边上的高最大,
当 AD过点 O时,AD最大,即:AD=AO OD= ,
△ABC面积的最大值= ×BC×AD= ×2OBsin60°× = ;
(2)如图 2,连接 OC,
设:∠OED=x,
则∠ABC=m x,∠ACB=n x,
则∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣m x﹣n x= ∠BOC=∠DOC,
∵∠AOC=2∠ABC=2mx,
∴∠AOD=∠COD ∠AOC=180°﹣m x﹣n x 2mx=180° m x﹣n x,
∵OE=OD,∴∠AOD=180°﹣2x,
即:180° m x﹣n x=180°﹣2x,
化简得:m﹣n 2=0.
【点评】本题为圆的综合运用题,涉及到解直角三角形、三角形内角和公式,其中(2),
∠AOD=∠COD ∠AOC是本题容易忽视的地方,本题难度适中.
10.【分析】(1)根据等边三角形的性质和圆周角定理解答即可;
(2)过点 A座 AG⊥BC于点 G,根据等边三角形的性质和勾股定理解得即可;
(3)①过点 E作 EH⊥AD于点 H,根据三角函数和函数解析式解得即可;
②过点 O作 OM⊥BC于点 M,根据相似三角形的判定和性质解答即可.
【解答】证明:(1)∵△ABC是等边三角形,
∴∠BAC=∠C=60°,
∵∠DEB=∠BAC=60°,∠D=∠C=60°,
∴∠DEB=∠D,
∴BD=BE;
(2)如图 1,过点 A座 AG⊥BC于点 G,
∵△ABC是等边三角形,AC=6,
∴BG= ,
∴在 Rt△ABG中,AG= BG=3 ,
∵BF⊥EC,
∴BF∥AG,
∴ ,
∵AF:EF=3:2,
∴BE= BG=2,
∴EG=BE BG=3 2=5,
在 Rt△AEG中,AE= ;
(3)①如图 1,过点 E作 EH⊥AD于点 H,
∵∠EBD=∠ABC=60°,
∴在 Rt△BEH中, ,
∴EH= ,BH= ,
∵ ,
∴BG=x BE,
∴AB=BC=2BG=2xBE,
∴AH=AB BH=2xBE BE=(2x )BE,
∴在 Rt△AHE中,tan∠EAD= ,
∴y= ;
②如图 2,过点 O作 OM⊥BC于点 M,
摄 BE=a,
∵ ,
∴CG=BG=x BE=ax,
∴EC=CG BG BE=a 2ax,
∴EM= EC= a ax,
∴BM=EM﹣BE=ax﹣ a,
∵BF∥AG,
∴△EBF∽△EGA,
∴ ,
∵AG= ,
∴BF= ,
∴△OFB的面积= ,
∴△AEC的面积= ,
∵△AEC的面积是△OFB的面积的 10倍,
∴ ,
∴2x2﹣7x 6=0,
解得: ,
∴ ,
【点评】此题是圆的综合题,关键是根据等边三角形的性质、勾股定理和相似三角形的
判定和性质解答.
11.【分析】(1)∠D=∠D,DE2=DB•DA,即可求解;
(2)由 ,即: ,即可求解;
(3)在△BED中,过点 B作 HB⊥ED于点 H,36﹣( ﹣x)2=( )2﹣x2,解得:
x= ,则 cos∠β= = ,即可求解.
【解答】解:(1)∵∠D=∠D,DE2=DB•DA,
∴△DEB∽△DAE;
(2)∵△DEB∽△DAE,
∴∠DEB=∠DAE=α,∵AB是直径,∴∠AEB=90°,又 AE=EF,
∴AB=BF=10,∴∠BFE=∠BAE=α,则 BF⊥ED交于点 H,
∵cos∠BED= ,则 BE=6,AE=8
∴ ,即: ,
解得:BD= ,DE= ,
则 AD=AB BD= ,
ED= ;
(3)点 F在 B、E、M三点确定的圆上,则 BF是该圆的直径,连接 MF,
∵BF⊥ED,∠BMF=90°,∴∠MFB=∠D=β,
在△BED中,过点 B作 HB⊥ED于点 H,
摄 HD=x,则 EH= ﹣x,
则 36﹣( ﹣x)2=( )2﹣x2,
解得:x= ,
则 cos∠β= = ,则 sin∠β= ,
MB=BF sin∠β=10× = ,
DM=BD﹣MB= .
【点评】此题属于圆的综合题,涉及了直角三角形的性质、相似三角形的判定与性质、
三角函数值的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合
能力要求较高,一定要注意将所学知识贯穿起来.
12.【分析】(1)令 y=0,可得 ax(x 6)=0,则 A点坐标可求出;
(2)①连接 PC,连接 PB延长交 x轴于点 M,由切线的性质可证得∠ECD=∠COE,
则 CE=DE;
②摄 OE=m,由 CE2=OE•AE,可得 ,由∠CAE=∠OBE 可得 ,则
,综合整理代入 可求出 的值.
【解答】解:(1)令 ax2 6ax=0,
ax(x 6)=0,
∴A(﹣6,0);
(2)①证明:如图,连接 PC,连接 PB,延长交 x轴于点 M,
∵⊙P过 O、A、B三点,B为顶点,
∴PM⊥OA,∠PBC ∠BOM=90°,
又∵PC=PB,
∴∠PCB=∠PBC,
∵CE为切线,
∴∠PCB ∠ECD=90°,
又∵∠BDP=∠CDE,
∴∠ECD=∠COE,
∴CE=DE.
②解:设 OE=m,即 E(m,0),
由切割线定理得:CE2=OE•AE,
∴(m﹣t)2=m•(m 6),
∴ ①,
∵∠CAE=∠CBD,
∠CAE=∠OBE,∠CBO=∠EBO,
由角平分线定理: ,
即: ,
∴ ②,
由①②得 ,
整理得:t2 18t 36=0,
∴t2=﹣18t﹣36,
∴ .
【点评】本题是二次函数与圆的综合问题,涉及二次函数图象与 x轴的交点坐标、切线
的性质、等腰三角形的判定、切割线定理等知识.把圆的知识镶嵌其中,会灵活运用圆
的性质进行计算是解题的关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/8/7 0:03:13;用户:初中数学;邮箱:13838033393;学号:26522812
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布 10.10
,




