容斥原理专门用于处理有“重叠”的计数问题,他的核心就是剔除重叠。解这类题目需要掌握容斥原理的核心考点,学会画文氏图,准确计算。
1.两集合容斥
所谓集合,就是具有某种相同属性的元素构成的整体,如把喜欢踢足球的人归为一个集合,可以表述为“喜欢踢足球的人”。每一个集合,可以画一个圆圈来表示,这就是“文氏图”。
两个集合的容斥原理内容如下图所示:

A∪B,读作“A并B”,表示或者属于A或者属于B的所有元素组成的集合。
A∩B,读作“A交B”,表示A与B共同的元素组成的集合。
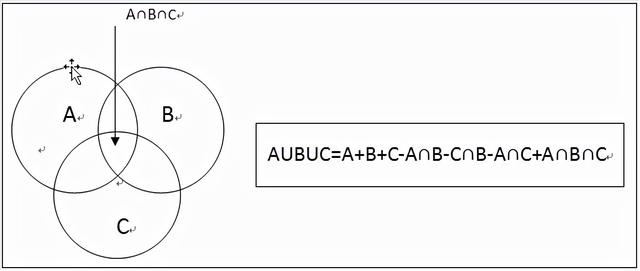
2.三集合容斥三集合的容斥原理内容如下图所示:

从上图可直观看出,总数被分成了七块,三块空白的“只属于其中某一个集合”、中间黑色的“属于三个集合”、三块灰色的“只属于其中某两个集合”。
于是又可以得到以下两个常用结论:
总数=只属于其中一个集合 只属于其中两个集合的 属于三个集合的
总数=三个集合之和-只属于其中两个集合的-2x属于三个集合的
3.多集合容斥极值求N个集合公共部分的最小值时,可利用如下公式求解:
A∩B数量的最小值=A B-I
A∩B∩C数量的最小值=A B C-2I
A∩B∩C∩D数量的最小值=A B C D-3I
注:I表示全体集合,多个集合的最小值可以此类推,依照上面公式进行计算。
在解决容斥问题时,往往需要通过画文氏图来梳理各集合间的关系,画文氏图时可直接将各数据标注到相应区域中。
,