上方超级数学建模可加关注
传播数学干货,学会理性的方式去思考问题
上一期还没介绍完说好的16篇就断了,今天势必介绍完再睡
7.集合论
对中学生读者来说,也许这是全书中最新颖的一篇。 集合可以分为有限集与无限集, 而我们通常所熟悉的自然数集只是最简单的一个无限集,即所谓的“可数的无限集”。 德国数学家康托尔发现,还存在“不可数的无限集”, 比如实数集。这里一个基本的概念是集合的势, 它是集合大小的度量,并允许我们比较任意两个集合的大小。 比如,我们说实数集比自然数集大,就是在下述意义下: 实数集的势大于自然数集的势。 在这里,康托尔提出了著名的连续统问题:是否存在一个集合, 其势比自然数集大,但比实数集小?这后来被希尔伯特列为著名的23个数学问题之首, 最终在1963年被科恩(P. J.Cohen)解决,答案是:在通常的 Z‐F 公理体系内,其真伪不能判定。
8.几个组合学的问题
9.华林问题
这是数论中有名的问题,对此已有许多优秀的通俗文章, 特别的,我们在此特别推荐笔者与北京交通大学博士生郑豪合写的文章。托普利兹与拉德梅彻在书中详细证明了著名的拉格朗日定理:每个正整数都可以写成四个自然数的平方和。
10.封闭自交曲线
11.数的素因子分解是否唯一?
算术(数论)一直是本书的一个主题,算术的基本定理断言:每个大于1的正整数可以唯一分解为素数的乘积。例如

12.四色问题
13.正多面体
这一篇用前一篇欧拉关于多面体的公式

14.勾股弦数与费马定理
也许最能简要体现出数与形之间的和谐关系的,当属勾股定理(国外称毕达哥拉斯定理):一个直角三角形的勾股弦三边长满足 。根据勾股定理的逆,满足的三个正数构成一个直角三角形的勾股弦。满足的三个正整数称为勾股弦数(国外称毕达哥拉斯三元数组)。古巴比伦数学家求出了所有的勾股弦数。
作者介绍了这一解法,并介绍了费马对


所作的不存在正整数解的著名论断(Fermat 最后定理, 1994年被英国数学家怀尔斯证明)。 作者介绍了费马对

无穷下降法是基于这样的想法:在自然数的有限集合中,不可能存在一个递减的无限序列。一个通俗的说法是:如果你银行卡上的钱是有限的,而且每天至少花掉一块钱但永远没有存入,那么存款迟早是要花完的。
15.算术与几何平均定理
16.有限点集的生成圆
这一篇与华林问题那一篇是笔者最喜欢的。本篇的结果归功于德国数学家 Heinrich Jung,在最简单的情况(平面情形),它断言:给定平面上一个有限点集(更一般的,对紧集也成立),如果该点集中两点之间的距离最大值为d(称为该集合的直径),那么存在一个半径为


17.用有理数逼近无理数
18.以连杆装置产生直线运动
19.完全数
20.素数无穷的欧拉证法
欧拉对素数序列的无穷性给出了一个高明的分析证法。他只用到三个事实:
第一,算术基本定理;
第二,等比数列的无穷和公式(可以认为阿基米德已经了解这一结果):

第三,调和级数

是发散的。 后一事实已经为欧拉的前辈雅各布·伯努利(JacobBernoulli)所知。
有鉴于这个证明的简洁优美,我们这里用现代记号复述一遍。
假定只存在有限多个素数




这就与调和级数发散的结论矛盾!当然,这里我们跳过了一些涉及无穷和的微妙细节,不过本质上这就是欧拉的思路。为避开无穷和对中学生可能引起的困难,只要考虑有限的部分和即可。
上述这个证明的要点在于,通过算术基本定理, 将求和与连乘积联系起来。事实上,这个想法可以给出著名的欧拉乘积公式:
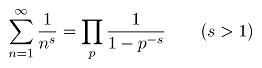
由此可以看到左边的级数(黎曼

21.极值问题的基本原理
这一篇强调了某些最大值问题可以有更简单的解法, 但因为作者在全书中都没有提到函数的概念,所以 他们并没有指出这样一个一般的原理。 现在的中学生早已接触函数的概念,所以我们不妨在这里稍作补充。
事实上,在许多极值问题的背后,隐藏着一个凸(凹)函数,于是,极值问题的求解成了著名的 Jensen 不等式的直接应用。对此我们稍作展开。
区间



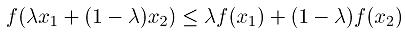
其几何含义是,函数的图像始终落在图像上两点连线的下方。类似的,如果函数的图像始终落在图像上两点连线的下方,即满足反向的不等式,则称为凹函数。例如,不难验证


对于凸函数,丹麦数学家 J.Jensen 在 1906 年发现了一个重要的不等式:
Jensen 不等式:设是
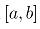



如果是上的凹函数,则相反的不等式成立。
现在根据 Jensen 不等式,不难推出,对于


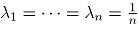

这个不等式就是“圆的所有内接n边形中,以正n边形的面积最大”这一几何事实的解析表达。
Jensen 不等式应用具体的凸(凹)函数可推导出许多著名的不等式, 例如第15篇的算术‐几何均值不等式。
22.定周长之图形的最大面积
这是著名的等周问题,因为作者考虑到本书是为高中生程度的读者写的,所以仅仅满足于证明: 在所有给定周长的平面图形中,如果存在一个面积最大的图形,那么该图形必定是圆。于是整个问题归结为证明最大值的存在性, 要说清楚这一点势必超出了中学生的理解水平, 因而作者只是点到为止(这在更高的水平上可以得到满意的处理)。\
23.循环小数
我们知道,分数可以化成有限小数或无限循环小数。 问题是:什么样的分数对应着有限小数; 而对于可以化成无限循环小数的分数,其循环节的长度是多少?对这些问题的回答,
需要用到初等数论。 作者在这一篇推导出著名的费马小定理以及欧拉的推广。
24.圆的特征性质
25.固定宽度的曲线
26.圆规在几何作图中之不可缺少性
这一节讲述了意大利数学家马歇罗尼(Mascheroni)的一个著名结果:用直尺和圆规作出的图,只需用圆规就可以作出。作者介绍了这个抽象结果的证明,不过有点遗憾的是,他们没有提供一个具体的例子。也许一个合适的例子是:仅用圆规将一个圆周四等分,据说这个例子就是马歇罗尼本人所解决的。我们留给有兴趣的读者。
27.数 30 的一个性质
28.一个改进的不等式
结语
我们以当代著名数学家盖伊(R. K.Guy)发表于30年前的《数学情报员》(MathematicalIntelligencer)的一篇题为《你是多好的数学工作者?》的文章中的一段话结束本文:
你是否读过并鼓励其他人读过这些书,比如 Courant 和 Robbins 的《数学是什么》, Steinhaus 的《数学万花筒》(Mathematical Snapshots); Rademacher 和 Toeplitz 的《数学欣赏》,Berlekamp,Conway 和 Guy 的《稳操胜券》(Winning Ways for yourMathematical Plays), Rouse Ball 的《数学游戏与欣赏》(Mathematical Recreations Essays), Martin Gardner 的著作,Dolciani 丛书,以及 the New Mathematical Library? 你是否曾将这些书作为礼物或奖品赠予对它们可能有兴趣的中学生或大学生?
via:林开亮老师(西北农林科技大学)
回复:数学欣赏
获取《数学欣赏》电子版
微信ID:超级数学建模(supermodeling)
数模君已和太白山果农联合推出数模君水果铺!!
点击阅读原文,当季水果任君选择!!!






