夜幕降临,华灯初上,快门声响起,一张记录城市夜色的照片透过屏幕跃然眼前:本应柔和的街灯发出了耀眼的光芒,代替星空为镜中城市增光添彩。

图1 城市夜景 (摄影设备与参数:Canon 70D, 67mm 8s, ISO 6400, f/25) 摄| 朱智敏
这有趣的现象激起了不少人的好奇:是什么光学现象创造了镜头下的星光?我们能否掌握其中的规律,自由地制造或者消除这种现象?
在基础光学早已成熟的今天,这个问题能够很好的用光学理论解决并进行仿真。如今,这类问题被统一归纳为星芒的现象来研究,接下来我们就将一探究竟。

图2 城市夜景 (摄影设备与参数:Canon 70D, 80mm 8s, ISO 6400, f/22) 摄| 朱智敏
★
波动光学与光的衍射
★
★
看到相片中的星芒后,有一定物理基础的同学就会判断这背后的原因是光的衍射,的确如此。在了解光的衍射现象之前,我们需要先从光的波动性说起。
最初的光学现在被整理为几何光学,即将光视为射线来研究光的反射、折射等问题。而在波动光学中,光被认为具有波动性,由此它获得了诸如波长、频率、周期、相位、波速等有关波的特征参数,并可以用波函数来描述。经典的光波函数形式如下:

上式用指数形式生动地体现了光波在空间及时间上的振荡特性。r 用来表示空间坐标位置,A(r)则代表该位置上光的振荡幅值。核心部分

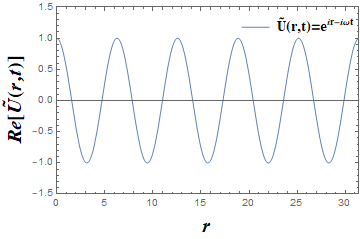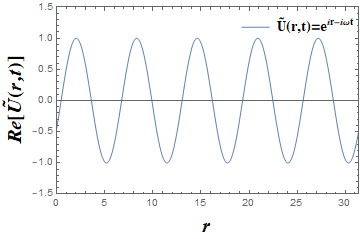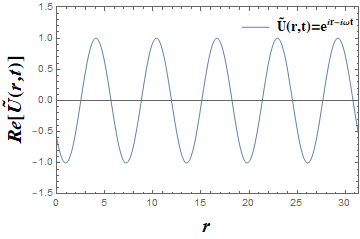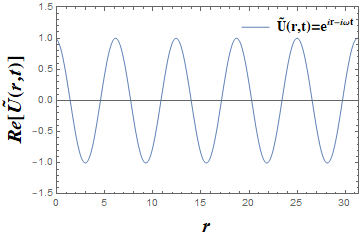
图3 在不同时刻下的一种简单的经典光波函数,A(r)=1,φ(r)=r 图| 朱智敏
波动光学提出了一个经典的物理概念——子波源与次波。要解释这个概念,可以想象水面泛起的波纹:中心振源在周围激起一圈涟漪,这圈涟漪随即在其周围激起一弧更大的涟漪,接着继续向外传播。在这个现象中,我们既可以认为只有中心波源一个波源在制造振动,也可以认为每圈涟漪上都存在着无数子波源——当涟漪被激发时,涟漪上的点振动起来,成为波源向外传递波动。

图4 水中涟漪 图源| pixabay
荷兰物理学家惠更斯用理论这样解释:波前上的每一点(面源)都是一个次级球面波的子波源,子波的波速与频率等于初级波的波速和频率,此后每一时刻的子波波面的包络就是该时刻出射波的波面;介质中任一处的波动状态是由各处的波动决定的。

图5 惠更斯原理示意图 图源| wikipedia
从子波源与次波的角度考虑,通过经典的光的单缝衍射实验,我们就可以很清晰地描述光的衍射。当光线垂直射向狭缝板时,打在板上的光波都会生成子波源,这些子波源以球面波的形式向外传递次波。当狭缝的尺度与入射光波长相当或更大时,狭缝附近那些本无法直线穿过狭缝的光线,就能通过这种激发出球面次波的方式,将光波传播到狭缝板的另一侧。这就像是光在传播过程中遇到了障碍物之后,绕过了障碍物继续传播。

图6 单色激光通过狭缝形成衍射的示意图 图源| wikipedia
而为了便于观察,使衍射光信号足够明显,我们一般要求狭缝的尺度尽可能小。
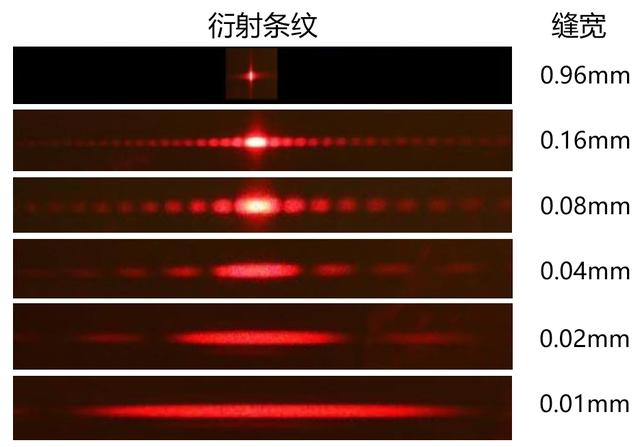
图7 缝宽对衍射条纹的影响 图源| 知乎https://zhuanlan.zhihu.com/p/208945796
按照接收屏距离狭缝的远近,衍射现象又分为夫琅禾费衍射(远场衍射)与菲涅耳衍射(近场衍射)。简单而言,两者的区别在于夫琅禾费衍射作为远场衍射可以忽略波函数中的一些高阶项简化计算。

夫琅禾费衍射积分式
★
相机成像中的衍射
★
★
我们究竟是如何通过相机获得星芒的图像的呢?相机的基本成像原理与光路是按照几何光学设计的,那么,这套几何光学系统是如何产生衍射现象的呢?
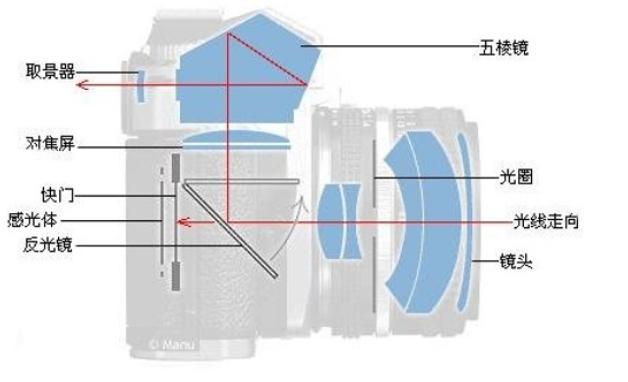
图8 单反相机的基本构造图。蓝色部分代表相机的光学器件。拍摄时按下快门,光线从相机的镜头汇入,经过无焦系统、光圈、聚焦镜头等前端光学系统后进入感光体(也称接收面)完成拍摄。图源| 知乎https://zhuanlan.zhihu.com/p/109956439
实际上,星芒现象的出现是光线通过光圈结构时发生了衍射现象。球面光透过无焦系统后变为平行光,平行光透过光圈发生夫琅禾费衍射,再透过聚焦系统,进入接收面被电子元件探测,最终被记录于相机的内存中。

图9 变焦相机简化系统示意图。相机中的无焦系统、光圈与聚焦系统三个光学器件共同影响入射光线的传播方式。图| 朱智敏
不同多边形的光圈拍摄出的星芒也不同,我们可以参考下图:

图10 部分光圈形状对应的星芒图样 图源| wiki commons
当多边形的直线边变为圆弧边时,星芒变为光束状;当光源透过圆形光圈时,星芒完全消失。由此,答案显而易见:衍射发生在边缘和夹角上;多边形的边越直,边角越多,光圈衍射产生出的星芒越发锐利丰富。
因此,如果想要避免星芒,可以使用没有边角的光圈或增大光圈;想要产生更多星芒,可以采用多边形光圈并适当缩小光圈。
而要想生成特定的星芒图样,就需要构造一个仿真系统,输入预想的光圈形状即可输出对应的星芒图样。这个仿真系统的主角正是前文提到的夫琅禾费衍射。
在大多数拍摄环境下,拍摄光源与相机的距离足够远,光圈中的衍射现象都可以用夫琅禾费衍射描述,回看夫琅禾费衍射公式:
这个积分式实际上是将光圈空间(x0,y0)通过傅里叶变换转换到接收面空间(x,y)。基于这个公式,我们在MATLAB软件中设计如下程序:假设白光由等光强的红绿蓝三色光组成,先输入光圈形状t(x0,y0),然后分别用不同颜色的光(即不同波长λ的光),对光圈进行傅里叶变换,得到夫琅禾费衍射图样,最后我们把三色光的结果叠加,得到对应的星芒形状(效果如图11),我们可以总结出n边形光圈与星芒的芒数N的关系:


图11 部分光圈形状对应星芒图样的仿真图像 图| 朱智敏
根据以上结果合理外推,我们能得到以下结论:偶数片光圈页片的镜头拍出来的星芒和光圈页片数相同,奇数页片的镜头拍出来的星芒数是光圈页片数的两倍。
★
摄影实战演练
★
★
有了理论解释,合格的物理学爱好者就该着手进行验证。我们准备了白炽灯作为光源、用Canon 70D相机,通过调整光圈大小进行了第一组实验。

图12 同一拍摄参数下不同光圈大小值所呈现的星芒图(1/2s,ISO100,光圈为7边形,白炽灯光源据相机焦平面1.9m)摄| 朱智敏
我们成功地用7边形的光圈获得了星芒数为14的星芒图像。并且光圈越大,星芒的可辨识度越小,这符合理论解释。但是你一定也能发现,当光圈过小时,星芒的效果同样不好。是什么原因导致了与理论相悖的结果?我们可以尝试调整曝光时间这一影响成像采样的因素来进行优化。
我们采用比图12中任何光圈都小的f/22,在经过足够长的曝光时间后,得到了非常好的星芒效果,成功解决了图12中的问题。

图13 同一拍摄参数下不同曝光时间所呈现的星芒图(f/22, ISO100,光圈为7边形,白炽灯光源据相机焦平面1.9m)摄| 朱智敏
如果我们更换不同形状的光圈镜头,缩小光圈,调整曝光时间,就可以获得不同形状的星芒图片(如图14),它们很好的验证了公式N(n)。

图14 不同光圈形状所拍摄的星芒 图源| pixabay
仿真结果很好地与实际成像吻合,由此,我们可以通过N(n)公式选择心仪的星芒形状,拍摄出对应的星芒点缀镜中的夜空。注意,要想拍出漂亮的星芒,还需要调整合适的光圈大小以及曝光时间哦。
来源:中国科学院近代物理研究所
,




