继续介绍传感器,为了保证内容的完整性,内容有些多了。大家可以关注,收藏。需要的时候拿出来看看。不知道什么时候就能用上了。
传感器的特性就是对输入输出关系的描述,理想的特性是在任何情况下输入与输出都是一一对应的。传感器的特性分静态特征与动态特征。
一、传感器的静态特性输入不随时间变化时(在稳态信号作用下),传感器输出与输入之间的关系。
1)、变换函数(静态特性的一般数学模型)
变换函数反映传感器输入与输出间的关系式, y=f(x)
其中x为输入量,y为输出量。几种典型的变换函数如下表

通常,要求传感器在静态情况下的输入与输出保持线性关系,实际上,如上表所示,很难满足理想的线性关系,一般用多项式表示
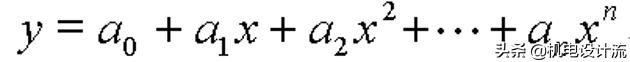
只有当二阶以上的项为0时,才满足理想的线性关系。
2、灵敏度(静态灵敏度)
当输入变化为Δx时,有:

其中k(x)称为灵敏度,是传感器在工作点上的微商(dy/dx),是静态特性的最主要指标。当k(x)为定值时,即Δy与Δx成比例,由测量值Δy便可直接求得Δx。 灵敏度具有可比性。
3、精度
传感器的精度是指测量结果的可靠程度,它以给定的准确度表示重复某个读数的能力,其误差愈小,则精度愈高。
定义为:传感器的精度表示传感器在规定条件下允许的最大绝对误差相对于传感器满量程输出的百分比,

其中,ΔA为测量范围内允许的最大绝对误差。
在应用中,为了简化传感器的精度的表示方法,引用了精度等级的概念,分为:0.05、0.1、0.2、0.3、0.5、1.0、1.5、2.0。精度等级越小精度越高 。
4、线性度(非线性误差)
在规定条件下,传感器校准曲线与拟合直线间最大偏差与满量程(F.S)输出值的百分比称为线性度。 线性度:

拟合方法有基端线性拟合、最佳直线拟合和最小二乘法拟合。

5、最小检测量和分辨率
是指传感器能确切反映被测量的最低极限量 Δx,小于这个量的区域称为死区。对于数字传感器,常用分辨率来表示。
最小检测量(或感度)的影响因素二:
1) 输入的变动量Δx在传感器内部被吸收
如:带有螺纹或齿条传递的传感器,由于螺纹和螺母间、齿轮和齿条间存在间隙,当输入变量Δx小于这一间隙时,便被传感器内部吸收。
2) 传感器输入、输出端均存在噪声干扰,Δx过小时,被外界噪声所淹没。
最小检测量:

其中,C为系数,一般取1~5,N为噪声电平,K为灵敏度。对于数字式传感器,则用输出数字指示值最后一位数字所代表的输入量来表示,称为分辨率。
6、滞后性
在输入量增加过程中测得的某一点输出值,与在输入减少过程测得的同一点值不一样,这种现象称为滞后。图中曲线称为滞环特性曲线。

对滞后性的衡量,一般用滞环的最大偏差或最大偏差的一半与满量程输出值的百分比来表示,称为滞环误差

如果传感器存在滞后性,则输入与输出就不能保持一一的对应关系,因此应尽量使之变小。产生滞后性的原因主要是材料的物理性质所造成的。
7、重复性
重复性是指在同一工作条件下,输入量按同一方向在全量程范围内连续变动多次所得特性曲线的不一致性。

不一致性一般用各测量值正、反行程标准偏差最大值的两位或三倍值与满量程输出值的百分比来表示(或称为回差)

其中,σ为标准偏差

8、零点漂移
传感器无输入(或某一输入值不变)时,每隔一段时间进行读数,其输出偏离零值(或原指示值),即为零点飘移,用百分比表示:

其中,Δy0为最大零点偏差(或相应偏差)。
9、温度漂移
温漂表示温度变化时,传感器输出值的偏离程度。一般以温度变化1℃时,输出最大偏差与满量程的百分比表示:

其中,Δmax为输出最大偏差,ΔT为温度变化范围。
二、传感器的动态特性传感器动态特性就是传感器的响应特性。传感器响应当输入信号随时间变化时, 输出信号随之变化的情况。
1、动态特性的一般数学模型
由于传感器在工作中,质量加速或减速需要时间,能量存取需要时间,信号在传输过程中克服阻力需要时间,所以输出信号总是要迟后输入信号,不可能同步变化。
动态特性的一般数学模型为一常系数微分方程:

式中,y(t)为输出信号,x(t)为输入信号,a0,a1,…,an及b0,b1,…,bm均为常数。
对上式两边进行拉氏变换,得

则得系统的传递函数如下

在一般情况下,上面的传递函数可以分解为分母 为一次多项式和二次多项式的分式形式,用一次多项式作分母的系统称为传递函数的一阶系统(即惯性环节),用二次多项式作分母的系统称为传递函数的二阶系统(即振荡环节)。所以一阶和二阶系统的响应是最基本的响应。
2、零阶传感器的数学模型
零阶传感器的微分方程只有a0、b0两个系数,方程为:

其中k为静态灵敏度,所以零阶系统的动态特性即就是系统的静态特性
典型的零阶系统如线性电位器

输出电压与电刷位移之间的关系:

3、一阶传感器的数学模型(惯性环节)
一阶系统的方程式为

其中(a1/a0)=τ,称为时间常数,(b0/a0)为静态灵敏度。
一阶系统函数(传递函数)

典型的一阶传感器如热电偶

微分方程如下:

其中:τ=Rmc,为热电偶的时间常数,
R 为介质与热电偶之间的热阻,
m 热电偶质量,
c 为热电偶的比热,
mc 为热电偶的热容量。
4、二阶传感器的数学模型(振荡环节)
二阶系统的微分方程为

二阶系统函数(拉氏传递函数)

式中

为静态刚度

为无阻尼固有频率

为阻尼比
上述三个量称为二阶传感器的特征量。典型的二阶传感器有光线示波器的振动子、铠装热电偶(即带保护套管的热电偶)。
5、传感器动态特征
时域方面采用瞬态响应法(阶跃响应),频域方面采用频率响应法(正弦响应)
(1)单位阶跃响应函数为

(2)一阶传感器的阶跃响应


时间常数

(3)二阶传感器的阶跃响应
二阶系统分欠阻尼系统(ξ<1)、过阻尼系统(ξ>1)和临界阻尼系统(ξ=1),一般传感器为欠阻尼系统,ξ值一般在0.7左右,其响应为


(4)传感器的动态特性频率响应:指在一系列不同频率的正弦信号的作用下,传感器的输出特性,分幅频特性和相频特性。

式中 A(ω)=|H(jω)|, φ(ω)=arctg[HI(ω)/HR(ω)]。
1)对正弦输入的响应(时域)
•若输入信号为正弦波:

则响应由暂态响应部分和稳态响应部分组成,暂态响应逐渐衰减直至消失,稳态响应是一与输入信号同频率但不同幅值,并存在相位差的正弦信号。
•一阶系统对正弦信号的响应为

其中:

二阶系统对正弦信号的响应为

式中 ω0——传感器无阻尼固有频率;
ωd——传感器有阻尼时的固有频率;
ξ——传感器阻尼比,
k1、k2,常数,由初始条件决定。
2)传感器的频率响应(频域)
传感器的频率响应函数(即传递函数)前面已进行了讨论
一阶系统的频率响应函数


幅频特性

相频特性
一阶系统的频率响应曲线


•二阶系统的频率响应函数


幅频特性

相频特性
•二阶系统的频率响应曲线






