本篇我们形象化的证明sinX的导数就是cosX
首先我们画一个单位圆,在单位圆上选取一个点,这个点经过的弧长是X,sin (x)是这个点的高
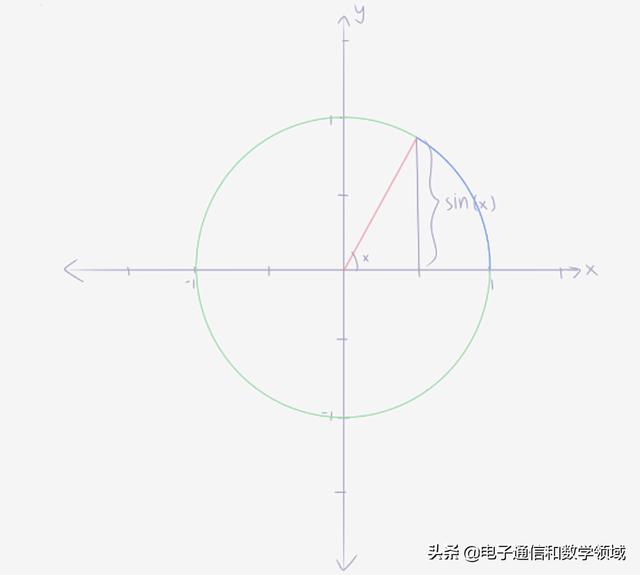
仔细观察圆上的这个点,考虑X值的微小变化dX,我们把增加的高度记作d(sin(x))。

因为d(x)基本上是一条直线,我们可以按如下方式作出一个直角三角形

现在,d(x)表示沿圆弧位置的微小变化,d(sin(x))表示新点的位置,也就是三角形高度的微小变化。
有趣的是,这个三角形恰好与原始点形成的三角形相似。这个新点形成的三角形夹角恰好等于X

记住sin(x)的导数表示高度变化量d(sin(x))和函数输入变化量d(x)的比值。当我们看这张图时,它等于角x的邻边比斜边

这个比值就是cos (x ),理解为什么sin(x)的导数是cos(x)本身就是一件很美妙的事情。
,




