【转载:丑陋却万能的二次方程求根公式 - 今日头条】https://m.toutiao.com/is/J3xHRDa/
这篇文章介绍了伟大的公式:二次方程求根公式。文中介绍了配方法,意犹未尽,我们接着从三个方面的应用来谈谈配方法。
在中学数学里配方法是极为重要的方法,它有十分广泛的应用。作为一个中学生,如果能熟练运用配方法,那么在面对不少数学问题的时候,就可以找到求解的途径了。
为何得名配方法?
用几何学的观点考虑把以下的方程配方:
x² bx=a
由于x²表示边长为x的正方形的面积,bx表示边长为b和x的长方形的面积,因此配方法可以看作矩形的操作。

什么叫配方法?
在数学中有一个简单公式就是:
(a b)²=a² 2ab b²
倒过来写,就是:
a² 2ab b²=(a b)²
等号右边是一个完全平方:(a b)²。等号左边含有三项:a²,2ab,b²。所谓配方法,就是在已知这三项中的某两项时,加上适当的一项(即“配”的意思),使得加上的一项与原有的两项的代数和恰为一个完全平方。


例如:

应用配方法时一定不要忘记:在加上某项的同时,必须同时减去这一项。否则,就不是恒等变形了。
小结:
配方法是一种代数的计算技巧,最主要的目的是把一个一元二次方程式或多项式化为一个一次式的完全平方,以便简化计算。
配方法应用之一:因式分解因式分解的方法很多,配方法就是其中的一个。请看下面的几道题目。
例1 试将x⁸ x⁴ 1进行因式分解。
解:x⁸ x⁴ 1
=x⁸ x⁴ 1 x⁴—x⁴
=(x⁴ 1)²—x⁴
=(x⁴ 1 x²)(x⁴ 1—x²)
对其中的前一个因式再进行配方:
x⁴ 1 x²
=x⁴ x² 1 x²—x²
=(x² 1)²—x²
=(x² 1 x)(x² 1—x)
∴ x⁸ x⁴ 1
=(x² x 1)(x²—x 1)(x⁴—x² 1)
在解题过程中除了完全平方公式,还用到了下图所示的平方差公式:
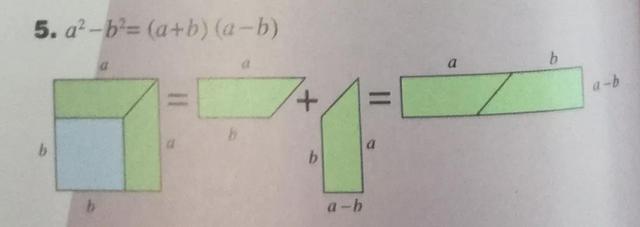
例2 试将x⁴ 324进行因式分解。
解:题目可以看作
(x²)² 18²,
因此中间的项是2(x²)18=36x²
所以有:
x⁴ 324=(x⁴ 36x² 324)—36x²
=(x² 18)²—(6x)²
=(x² 18 6x)(x² 18—6x)
=(x² 6x 18)(x²—6x 18)
最后一个步骤是把所有的项按降幂方式排列。
例3 试将x⁴ 4x²y²—32y⁴进行因式分解。
解:x⁴ 4x²y²—32y⁴
=x⁴ 4x²y² 4y⁴—4y⁴—32y⁴
=(x² 2y²)²—(6y²)²
=(x² 8y²)(x²—4y²)
=(x² 8y²)(x 2y)(x—2y)
例1和例2是配中间一项完成配方,例3是配第三项完成配方。
配方法应用之二:解方程先把方程的常数项移到方程的右边,再把左边配成一个完全平方式,如果右边是非负数,就可以进一步通过直接开平方法来求出它的解。
熟悉一元二次方程的读者一定能默写出它的求根公式吧!
当a≠0时,关于x的方程ax² bx c=0的根是

判别式Δ=b²—4ac
当Δ>0时,x₁≠x₂ 并且x₁与x₂都是实数。
当Δ=0时,x₁=x₂ 并且x₁与x₂都是实数。
当Δ<0时,x₁≠x₂ 但是x₁与x₂不是实数。
这个求根公式是初等代数学里一个完美的结果。有了它,可以求解任何一个一元二次方程,因此,它的重要性是不言而喻的。但是,我们不要忘记,这个伟大公式的导出,正是配方法的一大贡献,是应用配方法的结果。下面就是推导过程:

配方法不仅可以解一元二次方程,对于某些高于二次的方程,恰当运用配方法,也可以求解。请看下例:
例 证明方程x⁴—12x 323=0 没有实数根。
证明:由x⁴—12x 323=0,得
x⁴ 324=12x 1
x⁴ 36x² 18²=36x² 12x 1
(x² 18)²=(6x 1)²
∴ x² 18=±(6x 1),即
x² 6x 19=0,x²—6x 17=0
由于这两个方程的判别式Δ=b²—4ac的值都是负数(分别是—40和—32),可知它们的根都不是实数,因而方程x⁴—12x 323=0没有实根。
配方法应用之三:证明不等式灵活运用配方法,可以证明不等式。
下面给出的真题,是苏联莫斯科物理技术学院的入学考试题:
题 已知x是实数,求证
x⁸—x⁵ x²—x 1>0。
命题者给出的解答是:
由于x是实数,因此可以分三种情形研究:
①x是负实数;
②x是0;
③x是正实数。
当x<0时:
x⁵,x均<0,因而—x⁵,—x均大于0,又由于x⁸,x²均大于0
∴ x⁸—x⁵ x²—x 1>0。
当x=0时:
x⁸—x⁵ x²—x 1=1>0。
当x>0时,这个情形比较复杂,又分以下三种情况,即:
如0<x<1,则x²>x⁵,1>x,因而
x⁸—x⁵ x²—x 1
=x⁸ (x²—x⁵) (1—x)>0,
如x=1,显然有
x⁸—x⁵ x²—x 1=1>0。
如x>1,则x⁸>x⁵,x²>x,也有
x⁸—x⁵ x²—x 1>0。
这个解答无疑是严密的,但是对于多数初中生来说则不易掌握。
现在,我们用多数初中生都可接受的配方法来证明这个不等式。
证明一:

证明二:

证明三:

看,由于巧妙地运用了配方法,一道大学入学试题仅用初中数学知识就简单地解决了!
从中,我们得到一个启示:掌握知识,当然是多多益善,但更主要的要会灵活运用。
配方法还可以求极值,但限于篇幅,我们下次再谈。
科学尚未普及,媒体还需努力。感谢阅读,再见。
,




