学数学就像看连续剧,从小学到初中,从初中到高中,虽然新知识层出不穷,但如果仔细研究,会发现他们有内在关联。看电视剧,如果知道前因后果,就更容易理解人物关系和矛盾冲突啦。学数学也是一样,我们如果孤立的看知识点,就像在跳集看电视剧,自然容易犯糊涂啦。
本文提要:
一、因式分解的前世今生
二、图解因式分解
三、因式分解快速训练法
阅读时间:5~10分钟
我们在小学就见过因式分解的“前世”,现在让先一起回顾回顾吧。
1、整数乘法计算与质因数分解
整数乘法计算:2×2×2×3=24
质因数分解 :24=2×2×2×3

分解质因数
我们把24拆分成几个质因数相乘的过程就是质因数分解,它要求分到不能再分,这与因式分解的逻辑完全一致。说白了就是把乘法计算反过来,同时要求分出来的乘法因子必须都是质因数。举个反例:24=8×3,就是没有分解完,因为8还可以分为3个2相乘。
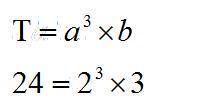
整式与整数计算
质因数:除了1以外,只能被它自己和1整除的正整数。
2、乘法分配律
乘法分配律:a(b c)=ab ac
除法分配律:(b c)÷a=b÷a c÷a (a不能为0)
这两个公式是不是非常眼熟,把他们等式的左右颠倒,不就是因式分解嘛?!
ab ac=a(b c)
这就是因式分解中的提公因式法啦,只不过我们小时候,都是用它来巧算。如图:

运用因式分解的巧算
再来说一说因式分解的今生,整式计算和因式分解是一对孪生兄弟。怎么说呢?一起看看吧。
3、整式乘除计算和因式分解
整式乘除,简单说就是A·B(A和B都是整式),因为整式有单项式和多项式,所以细分一下为:①单项式乘以单项式,②单项式乘以多项式,③多项式乘以多项式。同理,整式的除法A÷B(A和B都是整式):①单项式除以单项式,②多项式除以单项式。哈哈,好像绕口令~
大白话表达如图:

单项式乘单项式

单项式乘多项式

多项式乘多项式
因式分解是啥?一句话:把整式乘法计算反过来,分解成多个整式(不能再进行乘法拆分的整式)相乘的结构。
因式分解常见方法有三种:
1)提公因式法:把单项式乘多项式的计算过程反过来。

提公因式法
2)公式法:运用完全平方公式和平方差公式,把计算过程反过来。

公式法
3)十字相乘法,二项式乘二项式反过来。

十字相乘法
乘法的运算逻辑和图形面积的运算逻辑完全一致,因此我们能用矩形面积计算来模拟整式的乘法。这样的好处是非常直观,能够辅助理解计算原理。


1、利用脑科学,做到合理有效的训练
在讲述方法之前,先科普一个知识——神经髓鞘化。我们的大脑意识本质是脑神经内生物电流的传递。髓鞘包围有鞘神经纤维轴索的管状外膜,由髓磷脂构成,故又称髓磷脂鞘。
髓鞘化是形成记忆的一种方式,能增强细胞组织间的连接。“驾轻就熟”、“熟能生巧”、“老马识途”等就是髓鞘化的结果。髓鞘化是如何形成的呢?简单说就是不断重复正确的训练,才能构建出正确的髓鞘化神经回路。
因此,充分的运用大脑的髓鞘化机制,是我们快速掌握某项技能的核心要领!

2、完美的练习带来完美的结果

大量正确的训练,才能带来正确的结果。可是,我在教学中发现,很多学生在还没有熟练运用因式分解公式的时候,就开始大量快速练习,这可能会导致公式用混,还有各种层出不穷的错误。
如果我们一开始老是练习错误的方法。不好意思,错误的回路会变得非常强大,那你以后就总会在这里犯错。因此,用公式最最重要的是一定用对,这样我们的神经才会建立起越来越多正确回路。当不断地正确练习加粗神经回路,就相当于把它建成了高速公路,这时候你想不快都难!!!
因此核心要点是做正确!一开始可以慢,细细体会公式如何套用,通过不断地练习,高速路建好了自然会快起来,而且还很准确。
3、因式分解快速训练法
划重点:千万别死记硬背,不断地使用它,使用它,使用它!!!
训练方法:
1)每次写作业时,先把公式默写下来,先翻书确认写的对不对,不对马上修正。
2)把公式放在随时能看到的地方,做题时对照着公式来写题目。(考试时也可如此,先把公式默写下来)
3)开始做题,按如下方法思考。强调:整个过程都可以随时看你默写下来的公式。
这个式子能不能提公因式?
可以,先提出来。提出来后的有几项?
不可以,这个式子有几项?
两项都是平方项且相减→用平方差公式
三项且三项都同号→完全平方公式(A B)型
三项且中间项与平方项异号→完全平方公式(A-B)型
如果不符合完全平方公式怎么办?(A、B的关系和中间项对不上)用十字相乘法。
一开始训练,把细节写出来,别省步骤,刚开始慢,能有效地训练髓鞘化,让我们把任何一个细节都关注到,当逐渐熟悉,基本不出错的之后,再训练跳步骤。


4)看着公式来变形,不断地使用就会让公式越来越熟悉,这样训练,我们会慢慢体会到公式的变形要义,能够保证不用错公式。
如果能够每天做上15题,训练一周,你自然会看到变化~完全可以就地取材,在课本上选择题目,或者是从自己的家庭作业里选择。先保证做对,然后练习提速。
如果已经有一些错误的回路,修正方法还是类似的,用正确的方法来训练,直到正确方法的神经回路强于错误回路,这时候脑子就会自动走康庄大道啦~
以上主要说的是公式法的运用。关于因式分解十字相乘法,其实训练方法是一样的,只不过十字相乘会更加灵活,需要训练的是如何变化。我将在后面专门分享。
成功就是把复杂的问题简单化,然后狠狠去做。
欢迎关注圆周派讲数学,每天分享数学题目和学习方法,授人以鱼,亦授人以渔!