下午在看一个算法的时候,突然看到了一个关于圆周率的问题,如果问你圆的周长怎么算,你肯定毫不犹豫是2πR,但是π是怎么算出来的呢?估计我们都没有想过,所以我们看很多算法的时候,其实只是给了我们一个公式,其实和不懂差不多不是很大。
我来调用下我薄弱的数学细胞,简单来看一下。把一个圆如果展开,得到的就是圆的周长,即一个非精确值3.1415926。

我们来推算一下,下面的这个六边形,如果圆心为中心,那么半径是和六边形的边长度是一样的。假设半径长度是1,则六边形的边也是1。
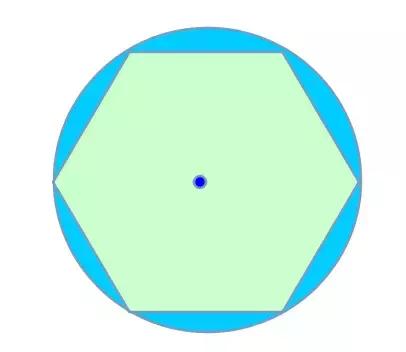
如果要求得圆周的长度,其实就是不断的把多边形扩张,一条边继续细分为两个角,即十二边形,如此类推,那么得到的结果就是一个极为精确的了。
然后换了个思路,重新来推导,总算有了起色。

所以我们可以很明确的知道,如果扩张后的长度和原来的长度的关系是这样的。那么我们就可以借助程序来实现圆周率的算法了。
当然假设我们是不知道圆周率这个东西的,在知道了这个关联关系后,其实可以继续做一些推导。
比如六边形,假设边长为x,则6x的长度是一个最粗略的圆的周长,这样一来,周长就是近似于6,它和半径的关系就是6*1,按照2πR的公式来看,其实也可以理解为2R(即为直径),当然实际周长要比6大一点。也就是我们计算π的意义了。
所以只要切分的边足够多,那么得到的π的值也就更加精确。这个时候写程序的话,可以参考如下的方式,不断的切分。
import java.util.Scanner; public class Test { public static void main(String[] args) { Scanner scan = new Scanner(System.in); System.out.println("请输入割圆次数:"); int n = scan.nextInt(); cut(n); }
static void cut(int n) { double y = 1.0; for (int i = 0; i <= n; i ) { double π = 3 * Math.pow(2, i) * y; System.out.println("第" i "次切割,为正" Math.round( 3 * Math.pow(2, i 1)) "边形,圆周率π≈" π); y = Math.sqrt(2 - Math.sqrt(4 - y * y)); } } }
程序的输出如下:
请输入割圆次数: 15 第0次切割,为正6边形,圆周率π≈3.0 第1次切割,为正12边形,圆周率π≈3.1058285412302498 第2次切割,为正24边形,圆周率π≈3.132628613281237 第3次切割,为正48边形,圆周率π≈3.139350203046872 第4次切割,为正96边形,圆周率π≈3.14103195089053 第5次切割,为正192边形,圆周率π≈3.1414524722853443 第6次切割,为正384边形,圆周率π≈3.141557607911622 第7次切割,为正768边形,圆周率π≈3.141583892148936 第8次切割,为正1536边形,圆周率π≈3.1415904632367617 第9次切割,为正3072边形,圆周率π≈3.1415921060430483 第10次切割,为正6144边形,圆周率π≈3.1415925165881546 第11次切割,为正12288边形,圆周率π≈3.1415926186407894 第12次切割,为正24576边形,圆周率π≈3.1415926453212157 第13次切割,为正49152边形,圆周率π≈3.1415926453212157 第14次切割,为正98304边形,圆周率π≈3.1415926453212157 第15次切割,为正196608边形,圆周率π≈3.1415926453212157
想象古代的人能够计算到小数点后7位,在条件那么简单的情况,真是厉害。
关于圆周率计算的方法,后续再花一些时间琢磨下,比如用蒙特卡洛的算法。今天给我最大的一个收获是让我真正做了一些计算,能够推导出一个看起来有些复杂的公式,看来小学初中的课程内容我开始熟悉起来了。
,




