动态规划算法求最小路径（动态规划求不同路径）

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例 1:

输入: m = 3, n = 2

输出: 3

解释:

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下

2. 向右 -> 向下 -> 向右

3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3

输出: 28

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10 ^ 9

动态规划解决

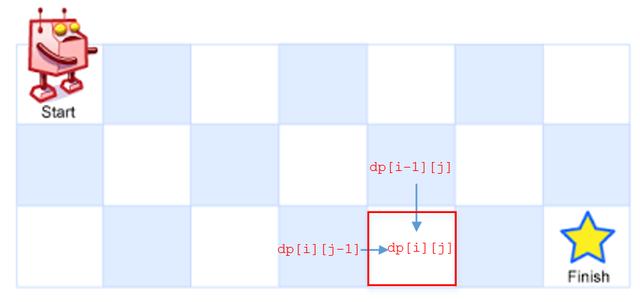
注意这里机器人只能向下和向右移动，不能往其他方向移动，我们用dp[i][j]表示到坐标(i，j)这个格内有多少条不同的路径，所以最终的答案就是求dp[m-1][n-1]。

因为只能从上面或左边走过来，所以递推公式是

dp[i][j]=dp[i-1][j] dp[i][j-1]。dp[i-1][j]表示的是从上面走过来的路径条数。

dp[i][j-1]表示的是从左边走过来的路径条数。

那么边界条件是什么呢，如果Finish在第一行的任何位置都只有一条路径，同理Finish在第一列的任何位置也都只有一条路径，所以边界条件是第一行和第一列都是1。我们已经找到了递推公式，又找到了边界条件，所以动态规划代码很容易写出来，我们来看下

publicintuniquePaths(intm,intn){ int[][]dp=newint[m][n]; //第一列都是1 for(inti=0;i<m;i ){ dp[i][0]=1; } //第一行都是1 for(inti=0;i<n;i ){ dp[0][i]=1; } //这里是递推公式 for(inti=1;i<m;i ) for(intj=1;j<n;j ) dp[i][j]=dp[i-1][j] dp[i][j-1]; returndp[m-1][n-1]; }

动态规划优化

我们看上面二维数组的递推公式，当前坐标的值只和左边与上面的值有关，和其他的无关，这样二维数组造成大量的空间浪费，所以我们可以把它改为一维数组。

publicintuniquePaths(intm,intn){ int[]dp=newint[m]; Arrays.fill(dp,1); for(intj=1;j<n;j ) for(inti=1;i<m;i ) dp[i] =dp[i-1]; returndp[m-1];8}

这里的dp[i] =dp[i-1]；实际上就是dp[i]=dp[i] dp[i-1]，我们可以这样理解，上面的网格我们是一行一行计算的，dp[i]也就是上面红色的表示的是当前位置上面的值，dp[i-1]表示的是当前位置左边的值。

递归方式

这题除了动态规划以外，还可以把上面的动态规划改为递归的方式

publicintuniquePaths(intm,intn){ returnuniquePathsHelper(1,1,m,n); } //第i行第j列到第m行第n列共有多少种路径 publicintuniquePathsHelper(inti,intj,intm,intn){ //边界条件的判断 if(i>m||j>n) return0; if((i==m&&j==n)) return1; //从右边走有多少条路径 intright=uniquePathsHelper(i 1,j,m,n); //从下边走有多少条路径 intdown=uniquePathsHelper(i,j 1,m,n); //返回总的路径 returnright down; }

代码中有注释，很容易理解，但其实这种效率很差，因为他包含了大量的重复计算，我们画个图来看一下。

我们看到上面图中红色，黑色，还有那种什么颜色的都表示重复的计算，所以有一种方式就是把计算过的值使用一个map存储起来，用的时候先查看是否计算过，如果计算过就直接拿来用，看下代码

publicintuniquePaths(intm,intn){ returnuniquePathsHelper(1,1,m,n,newHashMap<>()); } publicintuniquePathsHelper(inti,intj,intm,intn,Map<String,Integer>map){ if(i>m||j>n) return0; if((i==m&&j==n)) return1; Stringkey=i "*" j; if(map.containsKey(key)) returnmap.get(key); intright=uniquePathsHelper(i 1,j,m,n,map); intdown=uniquePathsHelper(i,j 1,m,n,map); inttotla=right down; map.put(key,totla); returntotla; }

使用公式计算

我们要想到达终点，需要往下走n-1步，往右走m-1步，总共需要走n m-2步。他无论往右走还是往下走他的总的步数是不会变的。也就相当于总共要走n m-2步，往右走m-1步总共有多少种走法，很明显这就是一个排列组合问题，公式如下

排列组合的计算公式如下

公式为(m n-2)! / [(m-1)! * (n-1)!]

代码如下

publicintuniquePaths(intm,intn){ intN=n m-2; doubleres=1; for(inti=1;i<m;i ) res=res*(N-(m-1) i)/i; return(int)res; }

总结

这题使用动态规划是最容易理解也是最容易解决的，当然后面的递归和公式计算也能解决。

如果喜欢这篇文章还可以关注微信公众号“数据结构和算法”，查看更多的算法题

,