常兴隆:数学思维中的数维
所谓简单结论——
观察下面的等式


这些等式告诉我们一个结论:
从1开始若干个连续自然数的立方和,等于这些自然数的和的平方。
只能这样吗?
让我们思考一个问题:
只有对于从1开始的连续自然数才有这个结论吗?
换一句话说, 我们还能找到其他的一些数,它们也满足立方和等于和的平方吗?
这样的数肯定可以找到,我们知道连续自然数1、2、3、4是满足这一规律的:

我们将其中的3改成2,发现1、2、2、4也满足这一规律:
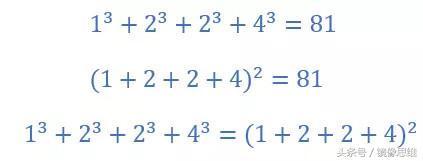
事实上,找到一两组这样的数,意义不大。关键是,能有什么规律性的发现。
诡异推广——
让我们注意数6,我们把它的因数按从小到大的顺序写出来:
1、2、3、6
我们再找出1、2、3、6的因数个数(即依次找出6的因数的因数个数):

这个地方有点绕,先按从小到大的顺序写出6的因数,再写出每个因数的因数个数。


1有1个因数,
2有2个因数,
3有2个因数,
6有4个因数。
请注意这些因数的个数:1、2、2、4
这就是上面提到的符合立方和等于和的平方的一组数。
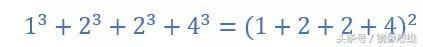
不只是6——
让我们再看一个数:12
写出它的因数,1、2、3、4、6、12
写出这些数的因数个数:1、2、2、3、4、6
就它们了:1、2、2、3、4、6
你会发现,它们的立方和等于它们和的平方。
似乎每一个数都对应着一组符合立方和等于和的平方这一规律的数。
连续自然数与谁对应?
我们来看看8:
写出它的因数:1、2、4、8
写出这些数的因数个数1、2、3、4
这样,我们发现,连续4个自然数对应8.
不只是8,如果你考虑27,也对应着1、2、3、4
事实上,27的因数:1、3、9、27
这些数的因数也分别是1、2、3、4。
8和27有什么共同点?
8是质数2的立方,27是质数3的立方。
一个质数的立方,对应着1、2、3、4
容易想到,一个质数的(n-1)次方,对应着1、2、3、…、n
为什么是这样?