一道高中立体几何题-求长方体的棱长之和
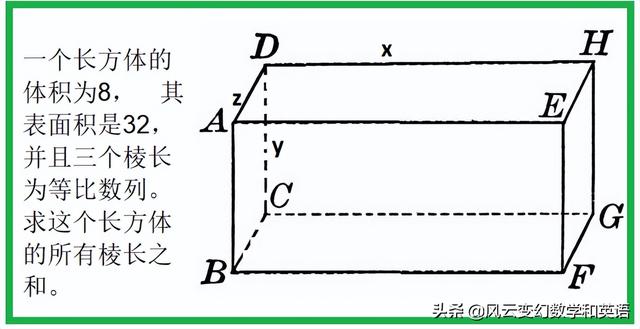
一个长方体的体积为8, 其表面积是32, 并且三个棱长为等比数列。求这个长方体的所有棱长之和。
解:
解法1:设三个不同的棱长为x, y, z, 那么根据已知的条件,
xyz=8,
2(xy yz zx)=32,
y·y=xz
将三个式子带入第一个中有:
y=2
因此xz=4,
再把y=2 和 xz=4 带入2(xy yz zx)=32,
可以得出:
2(xy yz 4)=32
即y(x z)=12,
所以x z=6,
因而x y z=8,
最后所有的棱长之和为:
4(x y z)=32
总结:一般来说在求某种代数式的值时,尽量不要求出其中的每个未知数,而用代数运算求出这个表达式为好。 下面的解法2显然比解法1要繁琐。
这道题如果求出x ,y 和z 的解是可行的,但有些情况下是不可求解的。
解法2:既然三个棱长为等比数列, 一般巧妙的方法是用两个数就可以表达三个等比数列, 设三个等比数列为:b/r, b, br
根据已知有:

解出b=2,
这样等比数列为2/r, 2, 2r,
带入表面积公式:
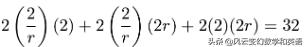
解这个方程:
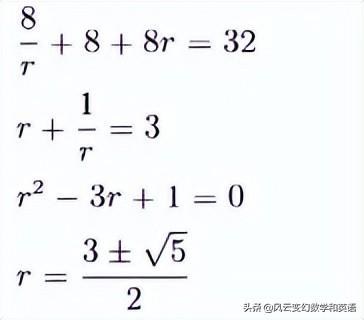
这里取一个r即可,只不过一个是递增,另一个递减,我们取加号的r值, 三个数为:

所以这三个数相加为:
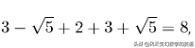
最后棱长的总和为4x8=32
,




