“问题是,我们到底是生活在哪个(数论)宇宙里?”
一个有零点,一个无零点。
在美籍华裔数学家、加州大学圣塔芭芭拉分校教授张益唐公开其关于朗道-西格尔零点猜想(the Landau-Siegel zeros conjecture)的最新研究论文前,这一零点将数论分成了上述两个宇宙。

张益唐教授11月8日上午面向北京大学师生和社会公众关于朗道-西格尔零点猜想的演讲
因为不知道这一零点到底存在不存在,数论学家们只好去讨论两种情况:如果这一零点存在,会得出什么结论?如果它不存在,会得出什么结论?
在三天前面向山东大学师生的演讲和11月8日上午面向北京大学师生和社会公众的演讲中,张益唐教授都多次提及其最新论文中证明朗道-西格尔零点猜想的创新思想或“New idea”(新方法)。
他同时表示,其论文还需要修改补充,更关键的是,要简化。新研究成果会对代数数论中的二次域的类数问题给出一个非常强的结果。
张益唐教授还在演讲中再次提及“大海捞针”。他说,与自己2013年发表的关于孪生素数猜想的研究突破相比,证明朗道-西格尔猜想才是真正的大海捞针。
11月8日上午,对于张益唐在演讲中提到的证明朗道-西格尔零点猜想的“New idea”(新方法),全程聆听该讲座的北京大学数学科学学院一位博士后向澎湃新闻(www.thepaper.cn)解释称,最简略地来讲,他是把计算中的z(n)序列,替换成了a(n)、b(n) 、c(n) 、d(n)序列,然后用柯西不等式推出矛盾,证明了在特定范围内不存在朗道-西格尔零点。
这位博士后进一步解释说,具体来说,张益唐教授在演讲中举了个例子,对于实连续函数来说,两个连续的零点之间函数取值是同号的,这样要证明零点在某个局部存在就等价于证明两个局部端点的函数值乘积非正,如果构造一个序列x(n)刻画出零点正负性的特征,那么证明x(n)中某一项为负就说明零点存在。同样的考虑实本原特征的黎曼ζ(Riemann zeta)函数,它的零点存在,也需要证明对于某个序列x(n),其中一项为负。传统的方法是,取一组实的z(n),考虑x(n)(z(n))^2的求和,如果为负,那么x(n)必存在一项为负。但传统的方法无法从一个无穷小量ε(epsilon)突破到0。张益唐教授的方法是,用a(n)、b(n)、c(n)、d(n)做两组求和,同时逼近;再使用柯西不等式,推出其中大小关系。这个工作的价值在于,将L(1,χ)的下界从无实效(not effective)的D的负ε次方,改进成实效(effective)的log D的负常数次方。
在演讲后的提问环节,有人问说,您所介绍的这种new idea,是看着“初等”,实际上是从非常深的工作中才提炼出来的,还是说是在大海捞针之后,直接用了一个初等的 idea去指导工作?
张益唐在回答这个问题时表示,“我的论文当然还要做很多修改和补充。可能更关键的是,要简化。否则的话,确实(令人)比较头疼。”
11月6日,菲尔兹奖得主詹姆斯·梅纳德(JamesMaynard)攻读博士学位时的导师、致力于解析数论领域的英国数学家、牛津大学数学研究所退休教授罗杰·希思-布朗(Roger Heath-Brown FRS)向澎湃新闻表示,“好好研读(张益唐的)这篇论文需要很长时间,所以我现在还不能说它是否正确。但它写得很清楚,而且策略明智。”
张益唐在演讲中说,“有的时候你说你用到了一些高深的东西,实际上从范围来讲,也没有超出复变函数的范围,但它有它的特殊处理方法。有些东西被弄得非常细腻,非常精致,所以它是一整套(方法)。就像我这个论文里,其实也有很多(这样的特殊处理方法)。最后有些东西我可能以后还得把细节补出来。有一些算术、有一些特殊的一些‘和’,我能够知道它的结果(的),基本上我也就给出声明了。但很多细节,现在说起来,写这些东西,对我来讲,还是很头疼了。”
张益唐表示,“这里严格讲起来,每一步都应该说都是初等的,但真正z(n)的选择,而且最后你要能够算出那个和,那就需要用到很多解析的工具。”
他还以菲尔兹奖得主塞尔伯格的研究为例称,“有时候初等比解析的东西更难,更有挑战性。”
还有人问起,关于朗道-西格尔猜想的研究突破在数论或算数几何中会有哪些应用?
张益唐回答,在数论里,它至少解决了一个目前为止还悬而未决的问题——“素数在等差级数中的分布”。“(如果)可能存在朗道-西格尔零点的话,那么在某些等差级数里,素数会特别多;在某些里头,素数会很少。我这个结果出来以后,至少把这个问题解决了。”
张益唐说,“在应用里头,因为是牵扯到解析数论,什么地方都得用到这个(结果)。”“还有一个,是代数数论里二次域的类数问题,这会给出一个非常强的一个结果。”
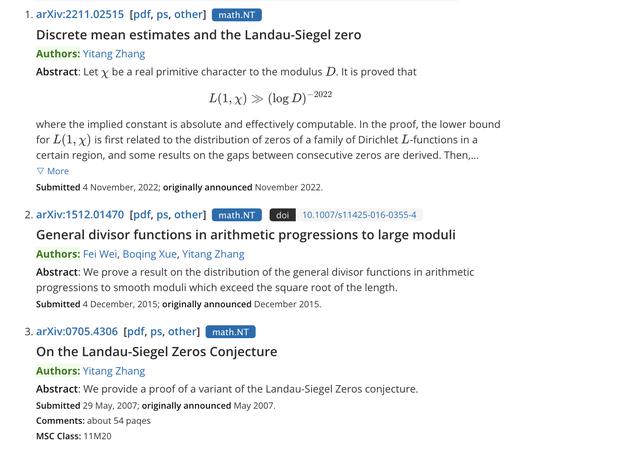
张益唐在网站arXiv上公开的三篇预印本论文
张益唐于2013年4月17日在《数学年刊》(Annals of Mathematics)发表《素数间的有界间隔》,首次证明了存在无穷多对素数对(p, q),其中每一对素数之差,即p和q的距离,不超过7000万。这为世纪难题“孪生素数猜想”的解决做出了突破性工作,他从一位默默无闻的大学讲师跻身世界重量级数学家的行列。随后,“7000万”这一数字,被数学界同行改进到600和246。
2007年5月29日,张益唐就曾在预印本网站arXiv提交了一篇标题为《论郎道-西格尔零点猜想》(On the Landau-Siegel Zeros Conjecture)的论文。该论文一共54页,正文13小节。该论文称,“我们提供了朗道-西格尔零点猜想的一个变体的证明。”
15年后,张益唐再次发布关于朗道-西格尔零点猜想的论文。在内部流出两天后,2022年11月7日,其最新论文在预印本网站arXiv上正式对外公开。论文的标题是《离散均值估计和朗道-西格尔零点》(Discrete mean estimates and the Landau-Siegel Zero)。全文111页,正文18个小节。
11月6日上午11:05,山东大学微信公众号发布了山东大学数学学院教授、博士生导师、原数学学院副院长、山东大学澳国立联合理学院执行院长吕广世、山东大学数据科学研究院教授、博士生导师黄炳荣等人联合撰写的文章。
该文章称,张益唐教授介绍了他在朗道-西格尔零点猜想研究方面的创新思想,在其最新预印本论文里证明了:模D的实原特征L-函数在区间(1−c(log D)^−2024,1】内没有实零点。
“如果把这里的2024换成1,就得到原始形式的朗道-西格尔零点猜想。2024虽然大于1,但在数学意义上,与1并没有实质性的差别。”山东大学微信公众号上述文章称。
20多天前,在美东时间10月14日下午8时(北京时间10月15日上午8时)举行的北京大学大纽约地区校友会的活动中,张益唐提前宣布了已解决朗道-西格尔零点猜想问题的消息。他说,要解决这一问题,最后归结到要做一个不等式;就是要构造一组数。“有人说孪生素数猜想是大海捞针,其实朗道-西格尔零点才是大海捞针。这些年来我试了无数种(情况),试数给代进去, 我建立了一整套公式,所以能去算。我试了无数种情况,每一次都差一个 ε(音:伊普西龙)。”
他说,他把“海底”查遍了,最后发现,不要这根针也能解决这一零点猜想问题。“我敢肯定地说,我做出来了。我知道我这么做是对的。”
在11月8日上午的演讲中,张益唐表示,在本质上,他已经证明了朗道-西格尔零点猜想。只是像他此前关于孪生素数猜想的研究结果一样,其结果可以被改进。这一最新研究突破将有很多应用,带来很多定理。
换句话说,张益唐的最新论文表明,在特定范围内,朗道-西格尔零点不存在。在这一情况下,朗道-西格尔零点猜想正确或成立。
“朗道-西格尔零点”被定义为广义黎曼猜想的反例。断言“朗道-西格尔零点”不存在的猜测,被称为朗道-西格尔零点猜想。
张益唐在演讲中同时表示,目前他把朗道-西格尔零点猜想的证明相关指数做到了2024,“比较庆幸。”这一结果可以被改进,但指数2024可以被改进到什么程度?“我想至少可以弄到几百吧。但弄到1?我的办法还是不够。”
张益唐教授的这一最新成果引起了数学界和社会公众的极大关注。这会不会成为其数学研究中的又一重要突破?有待数学界专家们的确认。
,