一、生活中的立体图形分类

1.棱柱的相关概念(初中只讨论直棱柱,即侧面是长方形)
①棱:在棱柱中,相邻两个面的交线叫做棱
②侧棱:在棱柱中,相邻两个侧面的交线叫做侧棱
③根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱......
④棱柱所有侧棱都相等,棱柱的上、下底面的形状相同,侧面的形状都是平行四边形
2.n棱柱的面、顶点、棱、侧棱、侧面数量关系
|
面 |
顶点 |
棱 |
侧棱 |
侧面 | |
|
三棱柱 |
5 |
6 |
6 |
3 |
3 |
|
四棱柱 |
6 |
8 |
12 |
4 |
4 |
|
五棱柱 |
7 |
10 |
15 |
5 |
5 |
|
n棱柱 |
n 2 |
2n |
3n |
n |
n |
3.点、线、面、体
①点:线和线相交的地方是点,它是几何中最基本的图形
②线:面和面相交的地方是线,分为直线和曲线
③面:包围着体的是面,分为平面和曲面
④体:几何体也简称体
⑤点动成线,线动成面,面动成体
二、展开与折叠
1.常见立体图形的展开图
①圆柱:两个圆,一个长方形
②圆锥:一个圆,一个扇形
③三棱锥:四个三角形
④三棱柱:两个三角形,三个长方形
⑤正方体展开图:共有11种,141(6种),231(3种),33(1种),222(1种)
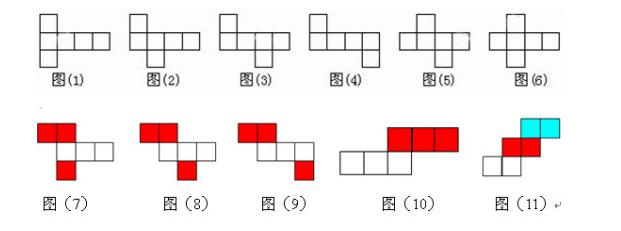
⑥要展开一个正方体,需要切开7条棱
⑦正方体平面展开图找对立面:相间、Z端
三、截一个几何体
1.常见立体图形的截面

2.用一个平面去截一个正方体,可能得到三边形、四边形、五边形、六边形(3456)
四、三视图(主视图、左视图、俯视图)
1.三视图的6种题型:
(1)已知实物图画三视图;
(2)已知俯视图,画主视图和左视图;
(3)已知主视图、左视图和俯视图,确定小立方体的个数;
(4)已知主视图和俯视图,确定小立方体最多和最少个数;
(5)已知左视图和俯视图,确定小立方体最多和最少个数;
(6)已知主视图和左视图,确定小立方体最多和最少个数。
五、多边形的一些规律
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个n边形分割成(n-2)个三角形。
2.从一个n边形的一边上的一点出发,分别连接这个点与其余各顶点,可以把这个n边形分割成(n-1)个三角形。
3.从一个n边形的内部的一个点出发,分别连接这顶点与其余各顶点,可以把这个n边形分割成n个三角形。
4.从一个n边形一个顶点出发,可引( n-3)条对角线,n边形共有条对角线。
5.数学家欧拉发现:若用f表示正多面体的面数,e表示棱数,v表示顶点数,则有:f v-e=2
第二章 有理数及其运算一、有理数
1.分类

有限小数和无限循环小数都是分数,都是有理数
2.正负数:表示相反意义的量
3.相反数
①只有符号不同的两个数叫做互为相反数,0的相反数是0
②在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等
③互为相反数的两个数的和是0。即a (-a)=0
4.数轴:规定了原点、正方向和单位长度的直线叫做数轴
①数轴三要素:原点、正方向、单位长度
②任何一个有理数都可以用数轴上的点表示。(反过来说不对,不能说数轴上所有的点都表示有理数)
③在同一数轴上,右边的数总比左边的数大
5.倒数
①乘积为1的两个有理数互为倒数(乘积为-1的两个有理数互为负倒数)
②如果a与b互为倒数,则有ab=1,反之亦成立
③倒数等于本身的数是1和-1。0没有倒数
6.绝对值
①在数轴上,一个数所对应的点与原点的距离,叫做该数的绝对值,记作
②任何数的绝对值总是非负数,即

③正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.
7.有理数比较大小
①正数>0>负数
②正数和正数比较大小,绝对值大的就大
③负数和负数比较大小,绝对值大的反而小
二、有理数的运算
1.运算顺序:先算乘方,再算乘除,最后算加减,有括号先算括号里面的
2.运算律
①加法交换律:a b=b a
②加法结合律:(a b) c=a (b c)
③乘法交换律:ab=ba
④乘法结合律:(ab)c=a(bc)
⑤乘法对加法的分配律:a(b c)=ab bc
3.有理数的加法法则
①同号两数相加,取相同的符号,并把绝对值相加
②异号两数相加,取绝对值较大数的符号,并用较大数的绝对值减去较小数的绝对值
③一个数同0相加,仍得这个数
4.有理数的减法法则
①减去一个数,等于加上这个数的相反数
5.有理数的乘法法则
①两数相乘,同号得正,异号得负,并把绝对值相乘
②任何数与0相乘,积仍为0
③几个不为0的因数相乘,积的符号由负因数的个数决定,当负因数的个数是偶数时,积为正;当负因数的个数是奇数时,积为负。
6.有理数的除法法则
①两数相除,同号得正,异号得负,并把绝对值相除
②0除以任何非0数都得0,0不可作为除数,否则无意义
③除以一个数,等于乘以这个数的倒数
7.有理数的乘方
①几个相同因数积的运算叫做乘方

②一个数可以看作是本身的一次方
③当底数是负数或分数时,要先用括号将底数括上,再在右上角写指数
④乘方的运算性质
⑴正数的任何次幂都是正数
⑵负数的奇数次幂是负数,偶数次幂是正数
⑶任何数的偶数次幂都是非负数,即
⑷1的任何次幂都得1,0的任何次幂都得0
⑸-1的偶次幂得1,-1的奇次幂得-1
⑹在运算过程中,首先要确定幂的符号,然后再计算幂的绝对值
8.科学记数法
①一般地,一个大于10的数可以表示成的形式,其中,n是正整数,这种记数方法叫做科学记数法。
第三章 整式及其加减一、字母表示数(字母可以表示任何数)
二、代数式
1.代数式的概念
用运算符号(加、减、乘除、乘方、开方等)把数与表示数的 字母连接而成的 式子叫做代数式。单独的 一个数或一个字母也是代数式。
2.注意
①代数式中除了含有数、字母和运算符号外,还可以有括号;
②代数式中不含有“=、>、<、≠”等符号。等式和不等式都不是代数式,但等号和不等号两边的式子一般都是代数式;
③代数式中的字母所表示的数必须要使这个代数式有意义,是实际问题的要符合实际问题的意义。
3.代数式的书写格式
①代数式中出现乘号,通常省略不写,如vt;
②数字与字母相乘时,数字应写在字母前面,如4a;
③带分数与字母相乘时,应先把带分数化成假分数后与字母相乘,如

④数字与数字相乘,一般仍用“×”号,即“×”号不省略;
⑤在代数式中出现除法运算时,一般按照分数的 写法来写,

注意:分数线具有“÷”号和括号的 双重作用。
⑥在表示和(或)差的 代差的 代数式后有单位名称的 ,则必须把代数式括起来,再将单位名称写在式子的 后面,

三、整式
1.单项式
①数与字母的乘积的形式的代数式叫做单项式,单独的一个数和一个字母也是单项式
②系数:单项式的数字因数叫做单项式的系数
③次数:单项式种所有字母的指数和叫做单项式的次数
2.多项式
①几个单项式的和叫做多项式
②项:组成多项式的每个单项式叫做多项式的项,不含字母的项叫做常数项
③次数:多项式中,次数最高的项的次数,叫做多项式的次数
3.同类项
①所含字母相同,并且相同字母的指数也相同的项,叫做同类项
②两个相同,两个无关
③合并同类项,把同类项合并成一项叫做合并同类项,系数相加,字母和字母的指数不变
4.去括号法则
①括号前面是 ,去掉括号和前面的 号后,原括号里各项的符号都不改变
②括号前面是-,去掉括号和前面的-号后,原括号里各项的符号都改变
5.添括号法则
①添“+”号和括号,添到括号里的各项符号都不改变
②添“-”号和括号,添到括号里的各项符号都要改变
6.整式的加减
一般步骤:先去括号,再合并同类项
第四章 基本平面图形一、直线、射线、线段

2.直线公理:经过两点有且只有一条直线(两点确定一条直线)
3.字母表示图形
①一个点可以用一个大写字母表示
②一条直线可以用一个小写字母或用直线上两个点的大写字母表示
③一条射线可以用端点和射线上另一点来表示(端点字母写在前面)
④一条线段可以用一个小写字母或用它的端点的两个大写字母来表示
4.点和直线的关系
①点在直线上,或者说直线经过这个点
②点在直线外,或者说直线不经过这个点
5.线段的性质
①线段公理:两点之间,线段最短
②两点之间的距离:两点之间线段的长度,叫做这两点之间的距离
③线段的中点到两端点的距离相等
④线段的大小关系和它们的长度的大小关系式一致的
6.比较线段的长短
(1)比较线段长短的两种方法:
①圆规截取比较法;
②刻度尺度量比较法.
(2)用刻度尺可以画出线段的中点,线段的和、差、倍、分;用圆规可以画出线段的和、差、倍
二、角
1.有公共端点的两条射线组成的图形叫做角,两条设想的公共端点叫做这个角的顶点
2.角也可以看成是一条射线绕着它的端点旋转而成的
3.角的表示
角的符号为“∠”
①用数字表示单独的角,如∠1,∠2,∠3等。
②用小写的希腊字母表示单独的一个角,如∠α,∠β,∠γ,∠θ等。
③用一个大写英文字母表示一个独立(在一个顶点处只有一个角)的角,如∠B,∠C等。
④用三个大写英文字母表示任一个角,如∠BAD,∠BAE,∠CAE等。
注意:用三个大写字母表示角时,一定要把顶点字母写在中间,边上的字母写在两侧。
4.角的度量
角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“°”表示,1度记作“1°”,n度记作“n°”。
把1°的角60等分,每一份叫做1分的角,1分记作“1’”。
把1’ 的角60等分,每一份叫做1秒的角,1秒记作“1””。
1°=60’,1’=60”
5.角的平分线
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线
三、多边形
1.由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形,叫做多边形
连接不相邻两个顶点的线段叫做多边形的对角线。
从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以画(n-3)条对角线,把这个n边形分割成(n-2)个三角形
四、圆
1.平面上,一条线段绕着一个端点旋转一周,另一个端点形成的图形叫做圆。固定的端点O称为圆心,线段OA的长称为半径的长(通常简称为半径)。
2.圆上任意两点A、B间的部分叫做圆弧,简称弧,读作“圆弧AB”或“弧AB”;由一条弧AB和经过这条弧的端点的两条半径OA、OB所组成的图形叫做扇形。顶点在圆心的角叫做圆心角。
第五章 一元一次方程
一、基本概念
(一)方程的变形法则
法则1:方程两边都 或 同一个数或同一个 ,方程的解不变。
例如:在方程7-3x=4左右两边都减去7,得到新方程:-3x=4-7。
在方程6x=-2x-6左右两边都加上2x,得到新方程:8x=-6。
移项:将方程中的某些项改变符号后,从方程的一边移动到另一边,这样的变形叫做移项,注意移项要变号。
例如:(1)将方程x-5=7移项得:x=7 5即x=12
(2)将方程4x=3x-4移项得:4x-3x=-4即x=-4
法则2:方程两边都除以或 同一个 的数,方程的解不变。

这里的变形通常称为“将未知数的系数化为1”。
注意:
(1)如遇未知数的系数为整数,“系数化为1”时,就要除以这个整数;如遇到未知数的系数为分数,“系数化为1”时,就要乘以这个分数的倒数。
(2)不论上一乘以或除以数时,都要注意结果的符号。
方程的解的概念:能够使方程左右两边都相等的未知数的值,叫做方程的解。
求方程的解的过程,叫做解方程。
(二)一元一次方程的概念及其解法
1.定义:只含有一个未知数,并且含有未知数的式子都是 ,未知数的次数是 ,这样的方程叫做一元一次方程。
例如:方程7-3x=4、6x=-2x-6都是一元一次方程。
而这些方程5x2-3x 1=0、2x y=l-3y、1/x-1=5就不是一元一次方程。
2.一元一次方程的一般式为:ax b=0(其中a、b为常数,且a≠0)
一元一次方程的一般式为:ax=b(其中a、b为常数,且a≠0)
3.解一元一次方程的一般步骤
步骤:去分母,去括号,移项,合并同类项,未知数的系数化为1。
注意:(1)方程中有多重括号时,一般应按先去小括号,再去中括号,最后去大括号的方法去括号,每去一层括号合并同类项一次,以简便运算。
(2)“去分母”指去掉方程两边各项系数的分母;去分母时,要求各分母的最小公倍数,去掉分母后,注意添括号。去分母时,不要忘记不等式两边的每一项都乘以最小公倍数(即公分母)
(三)一元一次方程的应用
1.纯数学上的应用:(1)一元一次方程定义的应用;(2)方程解的概念的应用;(3)代数中的应用;(4)公式变形等。
2.实际生活上的应用:(1)调配问题;(2)行程问题;(3)工程问题;(4)利息问题;(5)面积问题等。
3.探索性应用:这类问题与上面的几类问题有联系,但也有区别,有时是一种没有结论的问题,需要你给出结论并解答。
本章要求
1.会对方程进行适当的变形解一元一次方程:解方程的基本思想就是转化,即对方程进行变形,变形时要注意两点,一时方程两边不能乘以(或除以)含有未知数的整式,否则所得方程与原方程的解可能不同;二是去分母时,不要漏乘没有分母的项,一元一次方程是学习二元一次方程组、一元二次方程、一元一次不等式及函数问题的基本内容。2.正确理解方程解的定义,并能应用等式性质巧解考题:方程的解应理解为,把它代入原方程是适合的,其方法就是把方程的解代入原方程,使问题得到了转化。3.理解方程ax=b在不同条件下解的各种情况,并能进行简单应用:(1)a≠0时,方程有唯一解;(2)a=0,b=0时,方程有无数个解; (3)a=0,b≠0时,方程无解。4.正确列一元一次方程解应用题:列方程解应用题,关键是寻找题中的等量关系,可采用图示、列表等方法,根据近几年的考试题目分析,要多关注社会热点,密切联系实际,多收集和处理信息,解应用题时还要注意检查结果是否符合实际意义。5.几种常见的问题:和差倍分问题、等机变形问题、劳力调配问题、比例分配问题、数字问题、工程问题。
第六章 数据的收集与整理一、数据的收集
1.数据收集的方法
①直接方法:观察、测量、调查、实验灯
②间接方法:互联网查询、查阅文献资料等
二、普查和抽样调查
1.普查(为一特定目的而对所有考察对象所做的全面调查)
①总体:所考察的对象的全体
②个体:组成总体的每一个考察对象
2.抽样调查(为一特定目的而对部分考察对象所做的调查)
①样本:从总体中所抽取的一部分个体。只有抽样调查里,才有样本
②样本容量:从总体中抽取的个体的数量
③为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到
④总体中的每一个个体都有相等机会被抽到,这样的抽样方法是一种简单随机抽样
⑤抽样调查要注意:1.样本容量不能太少(广泛性);2.样本应具有代表性
注意:
①抽样调查时,采用不同的样本,得到的结果一般也不相同.要想得到总体较准确的结果,一方面样本要具有较好的代表性,同时样本容量要大一些.
②调查样本是按随机的原则抽取的,在总体中每一个单位被抽取的机会是均等的,因此,能够保证被抽中的单位在总体中的均匀分布,不致出现倾向性误差,代表性强。③抽样调查是以抽取的全部样本单位作为一个“代表团”,用整个“代表团”来代表总体。而不是用随意挑选的个别单位代表总体。④所抽选的调查样本数量,是根据调查误差的要求,经过科学的计算确定的,在调查样本的数量上有可靠的保证。
3.普查与抽样调查的比较

三、数据的表示
1.扇形统计图
利用圆与扇形来表示总体与部分的关系,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图。(各个扇形所占的百分比之和为1)
圆心角度数=360°×该项所占的百分比。(各个部分的圆心角度数之和为360°)
2.条形统计图
条形的高度表示某类别数据的个数,条形的高度越高,说明这类数据的个数越多
3.频数直方图
①各组中数据的个数叫做频数.
②频数与数据总个数的比值叫做频率.各组的频率之和为1.
③把所有数据分成若干个组,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距.
④把数据分成若干组,分成组的个数叫组数.

⑤频数分布表与直方图可以表示数据的分布情况.
4.折线统计图
5.统计图的选择
①条形统计图能清楚的表示出每个项目的具体个数
②折线统计图能清楚的反映出事物的变化情况
③扇形统计图能清楚的表示出各部分在总体中所占的百分比
,




