伟大而优秀的导师必定是谦和与博学共存的。索末菲喜欢用“nursery ”来描述他自己领导的慕尼黑大学理论物理研究所。“nursery”可翻译成“保育院”,这个词语本身便充分表明了索末菲对他培育的学生们无尽的欣赏和关爱。

撰文 | 张天蓉
量子力学之诞生与发展,在当年就已经引产了数十名诺贝尔奖得主。然而,赞赏之余有遗憾,物理学界量子之林中,也有几个光环没有照到的死角。任何奖项都不可能是绝对公平的,多数人是实至名归,但也有几个被“漏奖”的大鱼,令人扼腕叹息!德国物理学家索末菲(Sommerfeld,1868年-1951年)就是典型的一位。
我们先来列举一下,在本英雄传中出场过的物理高手们(他们的出生年显示于括号中):普朗克(1858)、维恩(1864)、瑞利(1842)、爱因斯坦(1879)、玻尔(1885)、汤姆逊(1856)、卢瑟福(1871)、朗道(1908)、居里夫人(1867)、让·佩兰(1870)、彭家勒/庞加莱(1854)、朗之万(1872)、德布罗意(1892)、M·布里渊(1854)。
这些人中大多荣获了诺贝尔奖,下图中将他们从左到右按照出生之年的顺序排列起来。图中也特别标志出索末菲对物理学的贡献,以及他培养出的学生中的诺贝尔奖得主们。
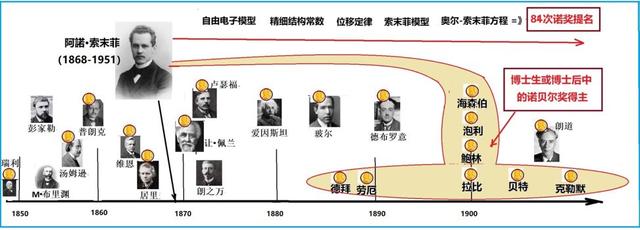
索末菲与诺贝尔奖
攻流体力学,与湍流纠葛
如今的科学界,没有人不知道爱因斯坦的名字,但却很少有人听过索末菲的名字。不过,如果我们穿越历史回到1900年左右,情况则是相反,那时的爱因斯坦只是个无名的专利局小职员,索末菲却已经是浪迹物理江湖多年的大教授了。那年头,普朗克正在思索黑体辐射之时,索末菲则企图攻克湍流的难题。
攻克湍流,谈何容易!这个领域至今也仍然是一个未解之谜,被称为是“经典物理学尚未解决的最重要的难题”。
索末菲比普朗克晚出生10年,比爱因斯坦早生10年。他们都是德国物理学家。索末菲出生于东普鲁士的柯尼斯堡,据说那是理论物理的发源地,诞生了许多知名人物,例如:大哲学家康德、作家霍夫曼、大数学家希尔伯特、数学家哥德巴赫、爱因斯坦大力称赞的女数学家诺特等等。甚至还有一个著名的“柯尼斯堡七桥问题”,也与该城市有关,大数学家欧拉因解决这个数学难题而创建了图论。
柯尼斯堡当年是德国文化的中心之一,有一种特殊的博学和文化的氛围。柯尼斯堡如今属于俄罗斯,叫加里宁格勒。索末菲诞生成长于一个如此的“风水宝地”,得天独厚,从小便沐浴于科学文化的阳光雨露中。索末菲在柯尼斯堡大学读书时,讲课的教授中便是数学大师云集,名师们的栽培和点拨,使他受益匪浅。之后他到哥廷根大学,又幸运地当上了数学家克莱因的助手。克莱因是研究非欧几何及群论之专家,在大众心目中,以熟知的拓扑例子“克莱因瓶”而著名。
大学的数学气氛如此浓厚,使索末菲的研究课题经常游走于物理与数学之间。在当时的德国,起初实验物理比理论物理更受重视,但后来,在这些精通数学的理论物理学家们(包括索末菲和波恩)的努力下,形势翻转过来,索末菲也因此而走上了数学上极其困难的“湍流研究”之路。
索末菲对湍流相关的流体力学的最主要贡献,是奥尔-索末菲方程(Orr–Sommerfeld equation)。索末菲认为,湍流的发生机理可以转化为一个稳定性分析问题。当流速高于某临界值时,层流变成不稳定,微小的扰动下即会产生湍流。奥尔-索末菲方程,是一个微分方程,通过解出方程,或者研究其特征值等,可以作为判断流体动力稳定性的条件。
然而,要解出这个方程是太困难了!索末菲自己也万没想到,这个方程,不仅后来困惑自己数年,也困惑自己的学生,以及整个物理界及数学界研究湍流的同行们多年。其中包括了海森堡开始时一无所获,后来凭直觉“猜”出答案, 20年后林家翘一举成功的生动故事等,此处不表。
索末菲对流体力学付出了几十年的心血和精力,湍流问题成了他一生的纠葛,直到高龄时都还经常耿耿于怀。二十世纪流体力学权威,钱学森、郭永怀等人的老师冯·卡门,在自传中记录了这样一段往事:“索末菲,这位著名的德国理论物理学家,曾经告诉我,在他死前,他希望能够理解两种现象——量子力学和湍流。” 海森堡对这段话的说法有点不同:“索末菲说过:见到上帝时我想问他两个问题:为什么会有相对论?为什么会有湍流?”
不管哪种版本,困惑索末菲一生,企图向上帝寻求答案的疑问中都包括了“湍流”一词,可见这个难题是何等地让他魂牵梦绕刻骨铭心的!
新原子模型,解释光谱线
除了思考湍流之外,索末菲以其深厚的数学功底,对狭义相对论的数学基础,以及电磁波在介质中的传播等课题,也作了重要的贡献。
对量子理论而言,索末菲也不愧为开山始祖之一。他本人的贡献主要是:改进了玻尔的原子模型,发现了精细结构常数。
玻尔1913年的原子模型,很好地解释了氢原子光谱线的分布规律,但仍然存在不少问题。一是进一步的实验结果发现,氢原子光谱线具有精细结构,原来的一条谱线实际上由好几条谱线组成;二是不能成功地解释除了氢原子之外的多电子的原子结构。
针对这些问题,索末菲在玻尔原子模型的基础上做了一些改进,建立了索末菲模型。索末菲的主要观点是认为电子绕原子核运动的轨道不一定是正圆形,而是椭圆形。玻尔模型中的圆形轨道对应于主量子数,而椭圆轨道的引入导致了另外的几个量子数。为此,索末菲首先提出了第二量子数(角量子数)和第四量子数(自旋量子数)的概念。

因为这些额外量子数的引入,使得电子轨道的能级不仅与主量子数n有关,也与角量子数l,以及自旋量子数s有关。此外还有一个第三量子数(磁量子数)m,是角量子数l在Z轴上的投影。它的作用表现在当原子受外磁场作用时的谱线分裂,即正常塞曼效应。其中三个量子数n、l、m,都取整数值,互相有制约。角量子数不能超过主量子数,磁量子数不能超过角量子数。而自旋量子数s,则只能取1/2和-1/2两个值。
精细结构常数,意义非凡
磁量子数可以解释正常塞曼效应,自旋量子数则可用于解释反常塞曼效应。从索末菲的原子模型可知:不同角动量量子数的轨道之间的能级差正比于某个无量纲常数的平方。索末菲在解释光谱的精细结构时引入了这个常数,即现在所说的“精细结构常数”。
引入精细结构常数后,原子模型中电子的运动速度和能级可以被表示成更为简洁的形式。之后,理论物理的发展,例如量子电动力学、统一理论等,将精细结构常数赋予了更深刻的含义,在世人面前展示了它的奇妙内涵。这是当初发现它的索末菲也未曾预料到的结果。
简单地说,精细结构常数是电磁相互作用中电荷之间耦合强度的度量,表征了电磁相互作用的强度。这个耦合常数的解读被扩充到其它的三种基本相互作用。换言之,每种相互作用都对应一个耦合常数,其数值的大小表征该相互作用的强度。例如:强相互作用的耦合常数约为1,大约是电磁相互作用的精细结构常数(1/137)的137倍,此外,弱相互作用的耦合常数约为10-13,引力相互作用的耦合常数为10-39。从这几个数值,大略可知四种相互作用强度之比较。
精细结构常数α,非常奇妙地将电荷e、普郎克常数h、以及光速c联系在一起:

这后面三个常数分别表征现代物理中三个不同的理论:电动力学、量子力学和相对论。它们(e、h、c)组成在一块儿构成了一个无量纲的常数α,即精细结构常数。问题是,常数α将这三个理论联系在一起,有什么深刻的奥秘吗?此外,常数α的数值约等于1/137,这又是什么意思呢?这个谜一样的数值多年来令物理学家们百思而不得其解,以至于关于它,物理学家费曼有一段十分有趣的话:
“这个数字自五十多年前发现以来一直是个谜。所有优秀的理论物理学家都将这个数贴在墙上,为它大伤脑筋……它是物理学中最大的谜之一,一个该死的谜:一个魔数来到我们身边,可是没人能理解它。你也许会说‘上帝之手’写下了这个数字,而我们不知道他是怎样下的笔。”
和蔼的同事,优秀的教师
量子力学的建立和发展,是一大批物理学家前仆后继辛勤耕耘的结果。当年的量子物理学界,能够在物理思想上被称之为“学派”的,实际上只有玻尔研究所的哥本哈根一家。其他的大师级别人物,有像普朗克、爱因斯坦那样的单打独斗者,也有如法国的德布罗意、英国人狄拉克等一类的散兵游勇之人。这些人只是时分时合,难以成“派”。
不过,索末菲所在的慕尼黑大学和波恩所在的哥廷根大学,虽然不像玻尔研究所那样,代表了量子理论中的一种具有特色的诠释,但也都有可观的理论物理中心,培养出了许多优秀的年轻物理学家,为量子理论作出了杰出的贡献。这三个地盘,其功劳是不可抹杀的,成为量子力学发展过程中的“黄金三角”。
索末菲在慕尼黑大学任教32年,兼任物理学院主任一职,他与同事和学生们都相处融洽,是一位善于发掘人才的优秀教师。玻恩曾说,索末菲的技能中包括对“天赋的发掘”。对此,爱因斯坦也曾经说:
“我特别佩服你的是,你一跺脚,就有一大批才华横溢的青年理论物理学家从地里冒出来。”
连泡利这样尖刻的“上帝的鞭子”,终其一生都对他的老师索末菲 “极度敬重”!据说只要索末菲走进他的屋子,泡利就会立刻站起,甚至鞠躬行礼。他对索末菲如此乖顺的举止,经常被习惯了“鞭子”抽打的弟子们传为笑谈。对此,有历史记载为证。
其一,奥地利物理学家韦斯科夫(Victor Weisskopf)在其自传中有过很有趣的记述:
“当索末菲来到苏黎世访问时, 一切就都变成了‘是,枢密顾问先生’……对于太经常成为他(指泡利)霸气牺牲品的我们来说, 看到这样一个规规矩矩、 富有礼貌、 恭恭敬敬的泡利是一件很爽的事情。”
其二,出于泡利本人的文字。索末菲 70 岁生日临近时, 泡利给索末菲写了一封信:
“您紧皱的眉头总是让我深感敬畏。自从 1918 年我第一次见到您以来, 一个深藏的秘密无疑就是, 为什么只有您能成功地让我感到敬畏。这个秘密毫无疑问是很多人都想从您那儿细细挖掘的, 尤其是我后来的老板, 包括玻尔先生。”

海森堡与泡利
索末菲是老派的德国教授,必定是十分注重礼仪的,也喜欢学生们在自己面前保持恭敬的礼节。但事实上,索末菲的威严中隐藏着和蔼,可以想象在讨论物理问题时,索末菲会把这些礼节都忘掉。正如埃克特(Michael Eckert)在他所作索末菲传记中总结的:
“普朗克是权威,爱因斯坦是天才,索末菲是老师。”
索末菲受聘于慕尼黑大学的记录中写着:“像玻尔兹曼、洛伦兹和维恩这样非常著名的理论物理学家”都支持索末菲,他被“描写为一位和蔼的同事和优秀的教师”。伟大而优秀的导师必定是谦和与博学共存的。索末菲喜欢用“nursery ”来描述他自己领导的慕尼黑大学理论物理研究所。“nursery”可翻译成“保育院”,这个词语本身便充分表明了索末菲对他培育的学生们无尽的欣赏和关爱。我把这句话表述成,慕尼黑物理学院是培养“理论物理学家的摇篮”!算一算索末菲众多的20多个颇有成就的学生们就明白了。

索末菲和玻尔
诺贝尔奖,有分无缘
量子力学的发展基本上有三个阶段:旧量子论、量子力学、量子场论。玻恩在1924年的一篇论文里开始呼唤新量子论的出现。没料到这个召唤还卓有成效,之后的2-3年内,量子论井喷式地蓬勃发展:德布罗意粒子波、海森堡矩阵力学、薛定谔波动力学、泡利原理、狄拉克方程……共同结束了旧量子时代,开创了量子新理论,即量子力学,吸引了无数年轻一代物理学家,也包括从索末菲的理论物理“摇篮”里,陆续“长大成熟”的学生们。
新量子论逐渐显示出它的巨大威力,薛定谔方程应用于氢原子,原来的玻尔-索末菲原子模型被薛定谔-玻恩电子云理论代替。不仅完美地重现了原来模型的结论,并且原来尚存的缺陷与不足,原未解决的困难问题,也都全部迎刃而解!稍后,狄拉克又在相对论的基础上,建立了描述高速运动微粒的相对论量子力学,成功地解释了自旋问题,亦促进了量子场论的建立。
那是一个充满传奇令人心潮澎湃的年代,物理新星不断涌现,年轻人荣获诺奖的故事司空见惯。索末菲桃李满天下,优秀导师成果累累。在他的正式博士生和其他受其影响的学生中,先后有7、8个人获得过诺贝尔奖, 几十人成为第一流的教授,在自己的专业领域内做出了重要贡献。
1914年,硕士生劳厄获诺贝尔物理学奖
1932年,博士生海森堡获诺贝尔物理学奖
1936年,博士生德拜获诺贝尔化学奖
1944年,硕士生拉比获诺贝尔物理学奖
1945年,博士生泡利获诺贝尔物理学奖
1954年,硕士生鲍林获诺贝尔化学奖
1962年,硕士生鲍林获诺贝尔和平奖
1967年,博士生贝特获诺贝尔物理学奖
诺贝尔奖也没有忽略像索末菲这样的老前辈。在1917年至1951年间,索末菲一共获得诺贝尔物理学奖提名84次,比其他任何物理学家都多。然而,也许毕竟是属于旧量子论最后的守卫者,难以超越量子领域中年轻的革命创新派,加上几次阴差阳错,命运作怪,索末菲最后仍然与诺奖无缘,只能被学界誉为“大师之师,无冕之王” 。
1951年4月26日,82岁的索末菲,与孙子外出散步时被车撞倒而意外去世,给世人留下无尽的遗憾。
,




