让我们先来了解一下我们的大脑是如何识别物体的。我们将学习什么是CNN, CNN如何利用大脑的启发进行物体识别,CNN是如何工作的。
让我们来了解一下我们的大脑是如何识别图像的
根据诺贝尔奖获得者Hubel和Wiesel教授的说法,视觉区域V1由简单细胞和复杂细胞组成。简单的单元有助于特征检测,而复杂的单元则结合了来自小空间邻域的多个这样的局部特征。空间池有助于实现平移不变特征。
当我们看到一个新的图像时,我们可以从左到右和从上到下扫描图像,以了解图像的不同特征。我们的下一步是结合我们扫描的不同的局部特征来对图像进行分类。CNN就是这样工作的
平移不变特征是什么意思?
图像的不变性意味着,即使图像旋转、大小不同或在不同照明下观看,对象也将被识别为同一对象。

这有助于对象识别,因为图像表示对图像变换(如平移、旋转或小变形等)保持不变。
我们使用卷积神经网络进行图像识别和分类。
让我们了解什么是CNN,以及我们如何使用它。
CNN是什么?CNN是Convolutional Neural Network卷积神经网络的缩写,卷积神经网络是一种专门用来处理数据的神经网络,它的输入形状类似于二维的矩阵图像。
CNN通常用于图像检测和分类。图像是二维的像素矩阵,我们在其上运行CNN来识别图像或对图像进行分类。识别一个图像是一个人,还是一辆车,或者只是一个地址上的数字。
和神经网络一样,CNN也从大脑中获取启发。我们使用Hubel和Wiesel提出的对象识别模型。
卷积是什么?卷积是一种数学运算,其中我们有一个输入I和一个参数核K来产生一个输出。
让我们用图像来解释。
我们有一个图像“x”,它是一个具有不同颜色通道(红色、绿色和蓝色RGB)的二维像素矩阵,我们有一个特征检测器或核“w”,然后应用数学运算后得到的输出称为特征图

这个数学运算有助于计算两个信号的相似度。
我们可能有一个特征检测器或滤波器来识别图像中的边缘,所以卷积运算将有助于我们识别图像中的边缘。
我们通常假设卷积函数在除存储值的有限点集外的任何地方都为零。

I是二维数组,K是核卷积函数
因为卷积是可交换的,我们可以把上面的方程重新写一下,如下图所示。我们这样做是为了便于在机器学习中实现,因为m和n的有效值范围变化较小。这是大多数神经网络使用的互相关函数。

以上是互相关函数
那么,我们如何在CNN中实现它呢?
我们实现它的方式是通过卷积层
卷积层是CNN的核心构件,它有助于特征检测。
核K是一组可学习的过滤器,与图像相比,它在空间上很小,但是可以扩展到整个输入图像的深度。
理解这一点的一个简单方法是,如果你是一名侦探,你在黑暗中看到一幅很大的图像或一幅画,你将如何识别图像?
你将使用你的手电筒和扫描整个图像。这正是我们在卷积层中所做的。
核K是一个特征检测器,它相当于图像I上的手电筒,我们正在尝试检测特征并创建多个特征图来帮助我们识别或分类图像。
我们有多个特征探测器,以帮助像边缘检测,识别不同的形状,弯曲或不同的颜色等事情。
这一切是如何运作的?
让我们取一幅3通道5×5矩阵的图像(RGB), 3通道3×3的特征检测器(RGB),然后以步长为1来扫描图像上的特征检测器。

当我在图像上应用特征检测时,输出矩阵或特征图的维数是多少?
特征图的维数与输入图像的大小(W)、特征检测器的大小(F)、步长(S)和图像的填充大小(P)有关
(W−F 2p)/S 1
在我们的例子中,W是输入图像的大小,为5。
F是特征检测器接受域大小,在我们的例子中,为3
步长(S)为1,图像上使用的填充大小(P)为0。
因此,我们的特征图维度为(5-3 0)/1 1=3。
因此特征图将是一个3*3的矩阵,有3个通道(RGB)。
下面一步一步进行解释

我们看到5×5的输入图像被简化为3×3的特征图,通道为3(RGB)
我们使用多个特征检测器来寻找边缘,我们可以使用特征检测器来锐化图像或模糊图像。
如果我们不想减少特征图的维数,那么我们可以使用如下所示的填充0
在这种情况下应用相同的公式,我们得到
(W−F 2 p) / S 1 => (5 - 3 2)/1 1= 5,
现在输出的尺寸将是5×5,带有3个颜色通道(RGB)。
让我们看看这一切是如何运作的
如果我们有一个3×3的特征检测器或滤波器,一个偏置单元,那么我们首先应用如下所示的线性变换
输出=输入*权重 偏差

参数个数 = (3 * 3 * 3) 1 = 28
对于100个特征检测器或过滤器,参数的数量将是2800。
在每一个线性函数的卷积运算之后,我们应用ReLU激活函数。ReLU激活函数在卷积层中引入了非线性。
它将特征图中的所有负像素值替换为零。
下图是应用ReLU激活函数后的特征图变换。

现在我们已经完成了局部区域的特征检测,我们将结合所有这些来自空间邻域的特征检测来构建图像。
记住你是一个在黑暗中扫描图像的侦探,你现在已经从左到右、从上到下扫描了图像。现在我们需要结合所有的特征来识别图像
池化我们现在应用池来获得平移不变性。
平移的不变性意味着当我们少量改变输入时,合并的输出不会改变。这有助于检测输入中常见的特征,如图像中的边缘或图像中的颜色
我们使用最大池函数,它提供了比最小或平均池更好的性能。
当我们使用最大池时,它总结了整个邻居的输出。与原来的特征图相比,我们现在有更少的单元。
在我们的例子中,我们使用一个2x2的框扫描所有的特征图,并找到最大值。
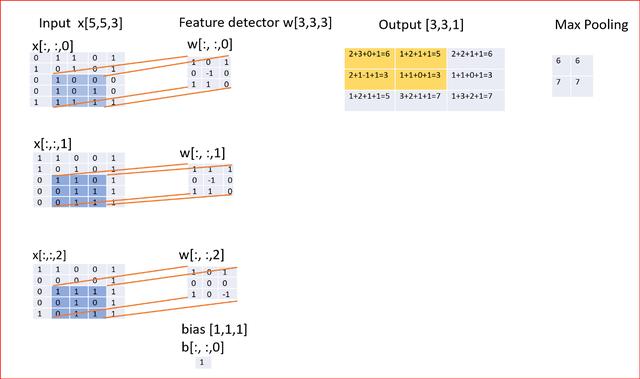
现在我们知道卷积网络由以下构成
- 并行的多重卷积,输出是线性激活函数
- 卷积层中应用非线性函数ReLU
- 使用像最大池这样的池函数来汇总附近位置的统计信息。这有助于“平移不变性”
- 我们将结果展平,然后将其输入到全连接神经网络
下图是完整的卷积神经网络

- 稀疏的交互
- 参数共享
- 等变表示
稀疏交互或稀疏权值是通过使用小于输入图像的核或特征检测器来实现的。
如果我们有一个大小为256 * 256的输入图像,那么就很难检测到图像中的边缘,因为其可能只占图像中像素的一个更小的子集。如果我们使用更小的特征检测器,那么当我们专注于局部特征识别时,就可以很容易地识别边缘。
另一个优点是计算输出所需的操作更少,从而提高了统计效率。
参数共享用于控制CNN中使用的参数或权值的数量。
在传统的神经网络中,每个权值只使用一次,但是在CNN中,我们假设如果一个特征检测器可以用来计算一个空间位置,那么它可以用来计算一个不同的空间位置。
当我们在CNN中共享参数时,它减少了需要学习的参数的数量,也减少了计算需求。
等变表示
这意味着目标检测对光照、位置的变化是不变的,而内部表示对这些变化是等方差的
,




