二次函数作为初中数学的核心内容,也是重要的基础知识和重要的数学思想方法,其自身结构特点和它在数学中的地位决定了:二次函数不仅与数学其他知识有着密切的联系,中将二次函数知识与我们的学习生活、经济发展、生产劳动等实际问题相结合的题型,在全国各地中考数学卷中更是倍受青睐。
因此,二次函数可以说是联系数学知识间或数学与实际问题间的纽带和桥梁,本文将着重分析的二次函数实际应用问题则是中考数学中不可或缺的重要内容。

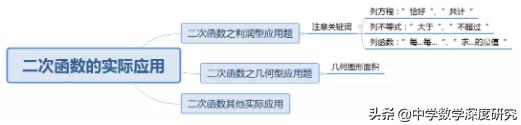
按照常考的实际问题种类,可将二次函数的实际应用分为:利润(营业额)最大问题、面积最大问题和实际抛物线问题。
下面,本文将通过经典真题重现的方式,对这三类问题进行试题分析,最后归纳与总结出解决这些问题的一般方法。
1、 利润最大问题
例1.(2019秋•武邑县校级期末)某校九年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为每千克8元,下面是他们在活动结束后的对话.
小丽;如果以每千克10元的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以每千克13元的价格销售,那么每天可获取利润750元.
(1)已知该水果每天的销售量y(千克)与销售单价x(元)之间存在一次的函数关系,请根据他们的对话,判决该水果每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系,并求出这个函数关系式;
(2)设该超市销售这种水果每天获取的利润为W(元),求W(元)与x(元)之间的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
(3)当销售利润为600元并且尽量减少库存时,销售单价为每千克多少元?
【分析】(1)依据题意首先确定学生对话中一次函数关系;
(2)根据销售利润=销售量×(售价﹣进价),列出平均每天的销售利润w(元)与销售价x之间的函数关系;
(3)依据函数的增减性求得最大利润.
【解答】:(1)当销售单价为13元/千克时,销售量为:750÷(13﹣8)=150千克,设y与x的函数关系式为:y=kx b(k≠0)
把(10,300),(13,150)分别代入得:k=﹣50,b=800,
∴y与x的函数关系式为:y=﹣50x 800(x>0).
(2)∵利润=销售量×(销售单价﹣进价),
根据题意得:
W=(﹣50x 800)(x﹣8)
=﹣50(x﹣12)² 800,
∴当销售单价为12元时,每天可获得的利润最大,最大利润是800元.
(3)将w=600代入二次函数W=(﹣50x 800)(x﹣8)=600,
解得:x₁=10,x₂=14(舍去),
即:当销售利润为600元并且减少库存时,销售单价为每千克10元.
【方法点评】本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.
这是一道与二次函数有关的实际应用问题,贴近生活,考生能学习生活知识,同时更帮助学生理解数学知识和生活之间的关系。研究题目,吃透题型是数学学习最有效,最实际的学习探究行为。从题目中挖掘知识点和方法技巧,提炼解题方法,概括题型,这样数学学习才能越学越有效,越学越轻松。
现代数学教育要求学生能体会数学与现实生活的紧密联系,增强应用意识,提高运用数学知识和方法技巧解决问题的能力。在近几年的中考数学试题中,经常出现与二次函数有关的实际应用问题,此类题型,有时候因其条件多,题目长,很多同学无从下手,难以快速找到解题思路。
变式1.(2019秋•余姚市期末)小颖家经营着一家水果店,在杨梅旺销季节,她的父母经常去果园采购杨梅用于销售.果园的杨梅价格如下:购买数量不超过20筐,每筐进价20元;购买数量超过20筐,每筐进价18元.小颖在观察水果店一段时间的销售情况后发现,当杨梅的售价为每筐30元时,每天可销售30筐;每筐售价提高1元,每天销量减少1筐;每筐售价降低1元,每天销量增加1筐.若每天购进的杨梅能全部售出,且售价不低于进价,从果园进货的运费为每天100元.
(1)设售价为每筐x元,则每天可售出 筐.
(2)当每筐杨梅的售价定为多少元时,杨梅的日销售利润最大?最大日利润是多少元?
【解答】:(1)根据题意得:每天可售出30﹣(x﹣30)=60﹣x[或30 (30﹣x)=60﹣x],故答案为:(60﹣x).
(2)设每筐杨梅的售价为x元,每天的杨梅销售利润为y,
①当60﹣x≤20,即x≥40时,y=(x﹣20)(60﹣x)﹣100=﹣x² 80x﹣1300=﹣(x﹣40)² 300
此时售价为40元,最大利润为300元;
②当60﹣x>20,即x<40时y=(x﹣18)(60﹣x)﹣100=﹣x² 78x﹣1060=﹣(x﹣39)² 341
此时售价为39元,最大利润为341元;
∵341>300,∴当每筐杨梅的售价定为39元时,
每天的杨梅销售利润最大,最大利润为341元.
变式2. (2019秋•东台市期末)某网店打出促销广告:最潮新款服装30件,每件售价300元,若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买2件,所买的每件服装的售价均降低6元.已知该服装成本是每件200元.设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)顾客一次性购买多少件时,该网店从中获利最多,并求出获利的最大值?
【解答】:(1)y=100x((0≤x≤10的整数);y=﹣3x² 130x(10⟨x≤30的整数);
(2)当0≤x≤10的整数y=100x,当10时,利润有最大值y=1000元;
当10˂x≤30时,y=﹣3x2 130x,
当x=-b/2a=65/3时,y取最大值,
因为x为整数,根据对称性得:当x=22时,y有最大值=1408元˃1000元,
所以顾客一次性购买22件时,该网站获利最多.
变式3. (2019秋•高邮市期末)5G网络比4G网络的传输速度快10倍以上,因此人们对5G产品充满期待.华为集团计划2020年元月开始销售一款5G产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第x个月(x为正整数)销售价格为y元/台,y与x满足如图所示的一次函数关系:且第x个月的销售数量p(万台)与x的关系为p=x 1.
(1)该产品第6个月每台销售价格为_______元;
(2)求该产品第几个月的销售额最大?该月的销售价格是多少元/台?
(3)若华为董事会要求销售该产品的月销售额不低于27500万元,则预计销售部符合销售要求的是哪几个月?
(4)若每销售1万台该产品需要在销售额中扣除m元推广费用,当6≤x≤8时销售利润最大值为22500万元时,求m的值.

【解答】:(1)设y与x满足如图所示的一次函数关系为y=kx b,
将(2,6500)、(4,5500)代入,得
k=﹣500,b=7500,
所以y=﹣500x 7500.
当x=6时,y=4500.
答:该产品第6个月每台销售价格为4500元;
故答案为4500;
(2)设该产品月销售额为w元,根据题意,得
w=py=(x 1)(﹣500x 7500)
=﹣500(x﹣7)² 32000
当x=7时,即该产品第7个月的销售额最大,
该月的销售价格是﹣500×7 7500=4000元/台;
答:该产品第7个月的销售额最大,该月的销售价格是4000元/台;
(3)根据题意,得
﹣500(x﹣7)² 32000=27500
解得x₁=4,x₂=10,
根据抛物线可知:
﹣500<0,抛物线开口向下,
销售该产品的月销售额不低于27500万元,
则预计销售部符合销售要求的是4、5、6、7、8、9、10月;
(4)根据题意,得当6≤x≤8时,共销售24万台,
扣除24m万元推广费用,
∴w=(x 1)(﹣500x 7500)﹣24m
=﹣500(x﹣7)² 32000﹣24m
32000﹣24m=22500
解得m=2375/6.
答:m的值为2375/6万元.
变式4.(2020•松滋市一模)金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:
(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.

【解答】:(1)①当12≤x≤20时,设y=kx b.代(12,2000),(20,400),
解得k=-200,b=4400,∴y=﹣200x 4400.
②当20<x≤24时,y=400.

(2)①当12≤x≤20时,
W=(x﹣12)y
=(x﹣12)(﹣200x 4400)
=﹣200(x﹣17)² 5000
当x=17时,W的最大值为5000;
②当20<x≤24时,
W=(x﹣12)y=400x﹣4800.
当x=24时,W的最大值为4800.
∴最大利润为5000元.
(3)①当12≤x≤20时,
W=(x﹣12﹣1)y
=(x﹣13)(﹣2000x 4400)
=﹣200(x﹣17.5)² 4050.
令﹣200(x﹣17.5)² 4050=3600
x₁=16,x₂=19,∴定价为16≤x≤19.
②当20<x≤24时,
W=400(x﹣13)=400x﹣5200≥3600,
∴22≤x≤24.
综上,销售价格确定为16≤x≤19或22≤x≤24.

二、面积最大问题
例2.(2019秋•宝安区期末)光明农场准备修建一个矩形苗圃园,苗圃一边靠墙,其他三边用长为48米的篱笆围成.已知墙长为a米.设苗圃园垂直于墙的一边长为x米.
(1)求当x为多少米时,苗圃园面积为280平方米;
(2)若a=22米,当x取何值时,苗圃园的面积最大,并求最大面积.

【分析】(1)根据题意得方程求解即可;
(2)设苗圃园的面积为y,根据题意得到二次函数解析式y=x(48﹣2x)=﹣2x² 48x,根据二次函数的性质求解即可.
【解答】(1):根据题意得:(48﹣2x)x=280,
解得:x=10或x=14,
∴当x为10米或14米时,苗圃园面积为280平方米;
(2):设苗圃园的面积为y平方米,则y=x(48﹣2x)=﹣2x² 48x=﹣2(x﹣12)² 288
∵二次项系数为负,∴苗圃园的面积y有最大值.
∴当x=12时,即平行于墙的一边长是24米,24>22,不符题意舍去;
∴当x=13时,y最大=286平方米;
答:当x=13米时,这个苗圃园的面积最大,最大值为286平方米.
【方法点评】本题考查了二次函数、一元二次方程、一元二次不等式的实际应用问题.解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.
变式1.(2019秋•瑞安市期末)如图,一面利用墙,用篱笆围成的矩形花圃ABCD的面积为Sm²,垂直于墙的AB边长为xm.
(1)若墙可利用的最大长度为8m,篱笆长为18m,花圃中间用一道篱笆隔成两个小矩形.
①求S与x之间的函数关系式;
②如何围矩形花圃ABCD的面积会最大,并求最大面积.
(2)若墙可利用最大长度为50m,篱笆长99m,中间用n道篱笆隔成(n 1)小矩形,当这些小矩形都是正方形且x为正整数时,请直接写出所有满足条件的x、n的值.

【解答】:(1)①由题意得:
S=x×(18﹣3x)=﹣3x² 18x(10/3≤x<6);
②由S=﹣3x² 18x=﹣3(x﹣3)² 27,
∴当x=10/3米时,S最大,为80/3平方米;
(2)根据题意可得:(n 2)x (n 1)x=99,
则n=3,x=11;或n=4,x=9,或n=15,x=3,或n=48,x=1.
变式2.(2019秋•雨花台区期末)某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG:BG=3:2.设BG的长为2x米.

(1)用含x的代数式表示DF=_______;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
【解答】:(1)∵区域①是正方形,区域②和③是矩形,
AG:BG=3:2.设BG的长为2x米,则AG=3x,
∴AP=GH=BE=PH=AG=3x,EH=GB=2x,
DC=PE=AB=5x,
∴DF=1/2(96﹣3×5x﹣3×3x)=48﹣12x.
故答案为48﹣12x.
(2)根据题意,得5x(48﹣12x)=180,
解得x1=1,x2=3
答:x为1或3时,区域③的面积为180平方米;
(3)设区域③的面积为S,
则S=5x(48﹣12x)
=﹣60x² 240x
=﹣60(x﹣2)² 240.
∵﹣60<0,∴当x=2时,S有最大值,最大值为240.
答:x为2时,区域③的面积最大,为240平方米.
变式3(2019秋•镇江期末)某兴趣小组想借助如图所示的直角墙角ADC(两边足够长),用20m长的篱笆围成一个矩形ABCD花园(篱笆只围AB、BC两边).
(1)若围成的花园面积为91m²,求花园的边长;
(2)在点P处有一颗树与墙CD,AD的距离分别为12m和6m,要能将这棵树围在花园内(含边界,不考虑树的粗细),又使得花园面积有最大值,求此时花园的边长.

【解答】:(1)设AB长为xm.由题意得:x(20﹣x)=91;
解得:x₁=13,x₂=7;
当x=13时,BC=20﹣13=7;
当x=7时,BC=20﹣7=13;
答:花园的边长为:13m和7m.
(2)设花园的一边长为x,面积为y.y=x(20﹣x)=﹣x² 20x=﹣(x﹣10)² 100,

解得:6≤x≤8,或12≤x≤14.
当x=8或12时,y有最大值为96,此时花园的边长为8cm或12cm.

三、实际抛物线问题
例3.(2019秋•汉阳区校级月考)有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数解析式;
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度.

【分析】(1)根据顶点坐标可设二次函数的顶点式,代入点(8,0),求出a值,此题得解;(2)利用二次函数图象上点的坐标特征,求出当y=1.8时x的值,由此即可得出结论;
(3)利用二次函数图象上点的坐标特征可求出抛物线与y轴的交点坐标,由抛物线的形状不变可设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣1/5x2 bx 16/5,代入点(16,0)可求出b值,再利用配方法将二次函数表达式变形为顶点式,即可得出结论.
【解答】:(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x﹣3)² 5(a≠0),
将(8,0)代入y=a(x﹣3)² 5,得:25a 5=0,解得:a=﹣1/5,
∴水柱所在抛物线(第一象限部分)的函数表达式为y=﹣1/5(x﹣3)² 5(0<x<8).
(2)当y=1.8时,有﹣1/5(x﹣3)² 5=1.8,
解得:x₁=﹣1,x₂=7,
∴为了不被淋湿,身高1.8米的人,站立时必须在离水池中心7米以内;
(3)当x=0时,y=﹣1/5(x﹣3)² 5=16/5.
设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣1/5x² bx 16/5,
∵该函数图象过点(16,0),
∴0=﹣1/5×16² 16b 16/5,解得:b=3,
∴改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣1/5x² 3x 16/5=﹣1/5(x﹣15/2)² 289/20.
∴扩建改造后喷水池水柱的最大高度为289/20米.
【方法点评】本题考查了待定系数法求二次函数解析式以及二次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数表达式;(2)利用二次函数图象上点的坐标特征求出当y=1.8时x的值;(3)根据点的坐标,利用待定系数法求出二次函数表达式.
变式1.(2019秋•西城区期末)图1是一个倾斜角为α的斜坡的横截面,tanα=1/2.斜坡顶端B与地面的距离BC为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系y=ax² bx(a,b是常数,a≠0),图2记录了x与y的相关数据

(1)求y关于x的函数关系式;
(2)斜坡上有一棵高1.8米的树,它与喷头A的水平距离为2米,通过计算判断从A喷出的水珠能否越过这棵树.
【解答】(1):在Rt△ABC中,tanα=1/2,BC=3,∴AC=6.
∴点B的坐标为(6,3).

所以水珠能越过这棵树.
变式2. (2018秋•无为县期末)如图,三孔桥横截面的三个孔都呈抛物线形,两个小孔形状、大小都相同,正常水位时,大孔水面常度AB=20米,顶点M距水面6米(即MO=6米),小孔水面宽度BC=6米,顶点N距水面4.5米.航管部门设定警戒水位为正常水位上方2米处借助于图中的平面直角坐标系解答下列问题:
(1)在汛期期间的某天,水位正好达到警戒水位,有一艘顶部高出水面3米,顶部宽4米的巡逻船要路过此处,请问该巡逻船能否安全通过大孔?并说明理由.
(2)在问题(1)中,同时桥对面又有一艘小船准备从小孔迎面通过,小船的船顶高出水面1.5米,顶部宽3米,请问小船能否安全通过小孔?并说明理由.

【解答】:(1)设大孔所在的抛物线的解析式为y=ax2 6,
由题意得,A(﹣10,0),
∴a(﹣10)² 6=0,∴a=﹣3/50,
∴大孔所在的抛物线的解析式为y=﹣3/50x² 6,
当x=2时,y=﹣3/50×2² 6=5.76>5,
∴该巡逻船能安全通过大孔;
(2)建立如图所示的平面直角坐标系,
设小孔所在的抛物线的解析式为z=mx² 4.5,
由题意得,C(3,0),
∴m×3² 4.5=0,∴m=﹣1/2,
∴小孔所在的抛物线的解析式为z=﹣1/2x² 4.5,
当x=1.5时,z=3.375<3.5,
∴小船不能安全通过小孔.

从以上3个不同类型的二次函数实际应用问题,我们不难发现,这类问题最终都能转化成求二次函数的最值问题。
我们还能总结出解决此类问题的一般方法:
①先求出实际问题中对应的二次函数的表达式(利润(营业额)最大问题和面积最大问题一般可以根据题意直接表示出二次函数的表达式,实际抛物线问题需要建立适当的直角坐标系再用待定系数法求解),需注意的是:若求出的二次函数表达式不是顶点式,需配方成顶点式;
②根据题意求出实际问题中自变量的取值范围;
③根据二次函数的图象和性质,结合②中求出的自变量的取值范围,最终解决问题。
在掌握了解题的基本步骤后,在解决实际问题时,还有2点尤其需要注意:
①善于将实际问题转化为数学问题,再转化为函数问题;
②注意自变量的取值范围,不仅保证函数解析式有意义,还要保证符合实际意义。
二次函数在我们的日常生活中应用广泛,《新课标改革》也强调要让学生感受到数学知识来源于生活,同时又服务于生活,充分认识到数学知识与现实生活中的实际问题联系紧密。
应用二次函数解决实际问题,对学生的逻辑思维等能力要求较高,加上一些学生知识面过窄,缺乏生活经验,对所学知识不能灵活应用等原因,总是拿不到高分。
因此,考生要想提高此类问题的解决能力,就必须要细心观察生活,增强应用意识,会分析一些现实生活中的实际问题与数学之间的关系,提高运用数学知识、建立模型等方法解决问题的能力。
,




