今天我们要讲一下数学中的“十字绣”绣布问题。看题目你以为我会教你十字绣?哈哈哈,当然不是,毕竟数学加小编是一个专业的数学编辑,像十字绣这种心灵手巧的活儿小编可干不来。只是恰好这两天在数学加看了张昊宇老师的奥数小课堂,突然受启发想到十字绣,十字绣的绣布呈网格状,每个小方格都是一样大小的,这些小方格正是绣好十字绣的关键!而今天,小编要带大家认识数学中的“绣布”——格点,它也对求图形面积起着很重要的作用!

一、认识格点
“数学上把在平面直角坐标系中横纵坐标均为整数的点称为格点。”这是百度百科对格点的定义,也是格点的专业定义。用小编的话来说:“一张方格纸上,上面画着纵横两组平行线,相邻平行线之间的距离都相等,这样两组平行线的交点,即所谓的格点。”如果你还是觉得很抽象,没关系,看下图!(红色的点即为格点)

二、格点与面积
如前文提到,格点对求图形面积有很大的帮助,在此之前,我们先介绍“格点多边形”的定义和一个著名的定理——皮克定理。
格点多边形:一个多边形的顶点如果全是格点,这个多边形就叫做格点多边形。
皮克定理:格点多边形面积=图内格点个数 周界格点数÷2-1。
例1、求格点图中图形的面积,其中每两个格点间的距离是1。

这个图是由3个独立的格点多边形组成的。
左边三角形面积可以用皮克定理求出:4 4÷2-1=5;
右边三角形面积可以用皮克定理求出:2 6÷2-1=4;
下面长方形长为6、宽为3,可以直接用长方形面积公式算出面积:6×3=18;
所以上图总面积为:5 4 18=27。
以上只是用皮克定理就能简单的求出格点图形的面积,虽然很适用,但是小编觉得还不够,小编恨不得将自己毕生所学都告诉你们(快要控制不住自己的洪荒之力)!!!接下来小编将结合“图形的割补”以及“等积变换”的知识点来求格点图中的面积。图形的割补在之前“巧求面积”的文章中提过,所以我们简单介绍一下“等积变换”的知识点。

小编只是知识的搬运者,上图是我们数学加张昊宇老师的课堂,他说:“等积变换的‘积’是指乘积(三角形底和高的乘积),如图中平行线,由于平行线之间距离相等,所以三角形ABC的高和三角形ABD的高是相等的,由于同底等高则两个三角形面积相等。”所以,在两条平行线中,无论把顶点C沿着平行线移至D点、E点还是F点,所得三角形的面积始终不变。好啦,有了以上的知识储备,我们一起来从题中体会。
题目:如图所示,图中五个方格边长均为1,求三角形面积。

方法1:运用皮克定理,三角形内有3个格点,边界上有3个格点,所以三角形的面积是

方法2:补!如图,把五个方格补成一个网格图。

所以三角形的面积可以用大正方形的面积减去三个三角形的面积。由于每个方格的面积是1,所有大正方形的面积是9,我们再看三个小三角形的面积分别是多少。

黄色三角形:黄色区域刚好是两个小方格组成的长方形的一半,故面积为1。
蓝色三角形:蓝色区域是六个小方格组成的长方形的一半,故面积为3。
绿色三角形:绿色区域是底部三个方格组成的长方形的一半,故面积为1.5。
所以,所求三角形的面积为9-1-3-1.5=3.5。
方法3:割!如图,将所求三角形割成三个小三角形。
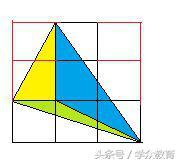
黄色三角形:两个方格的一半,面积为1。
蓝色三角形:(注意这里我们就要用的刚才介绍的等积变换了)如下图所示,把三角形右下角的顶点移至右上角,得到的黑色三角形的面积与原蓝色三角形面积是相等的,由于黑色三角形是四个方格的一半,所以面积为2,即蓝色三角形的面积为2。

绿色三角形:同样用等积变换的道理,把三角形右下角的顶点移至左下角,得到的黑色三角形的面积与原绿色三角形面积相等,是一个方格的一半,所以绿色三角形的面积是0.5。
综上所述,所求三角形的面积是1 2 0.5=3.5

阿基米德说:“给我一个支点我能撬动地球。”数学加编辑说:“给你一张网格,你能求出万千图形面积。”之前的文章我们就强调面积在生活中的重要性,而格点又为求面积带来不少方法,知识是无穷尽的,数学总是有用的,“好好学习,天天向上”这句话一定是没错的!加油吧少年!






