上一章《python递归与迭代:N级楼梯,每次只能跨1或2级,共有几种走法?》,我使用了数学递推法来解题,并通过python使用递归算法、迭代算法来计算解题。今天,我将跟大家一起探讨和使用数学中的排列组合方法一起解题。
排列组合知识点复习:
1、在数学中,从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号A(n,m)表示
2、从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示
3、组合数公式:
解题思路:
1、先抽取一个N=3的情况,穷举所有走法进行观察。用队列list把每次跨过的阶梯数记录下来,跨1级记录为数值1,跨2级记录为数值2。
N=3级楼梯走法:
1、如每次走1级,则 list=[1,1,1]
2、如第1次走2级,第2次走1级,则 list=[2,1]
3、如第1次走1级,第2次走2级,则 list=[2,1]
上述过程中有3个不同 list,所以3级楼梯走法共有 3 种
2、从上述步骤1中,可以看出,有多少个list,就有多少种走法,记为F(N)
3、再抽取一个N=5的情况,穷举所有走法进行观察,记录数值2的元素个数x 和 list长度(即list中元素的数量)关系,确定x的取值范围。
N=5级楼梯走法:
1、list=[1,1,1,1,1], 数值2的元素个数x=0,list长度=N=5
2、list=[2,1,1,1], 数值2的元素个数x=1,list长度=N-x=5-1=4
3、list=[1,2,1,1], 数值2的元素个数x=1,list长度=N-x=5-1=4
4、list=[1,1,2,1], 数值2的元素个数x=1,list长度=N-x=5-1=4
5、list=[1,1,1,2], 数值2的元素个数x=1,list长度=N-x=5-1=4
6、list=[2,2,1], 数值2的元素个数x=2,list长度=N-x=5-2=3
7、list=[2,1,2], 数值2的元素个数x=2,list长度=N-x=5-2=3
8、list=[1,2,2], 数值2的元素个数x=2,list长度=N-x=5-2=3
上述过程中,x取值范围为:0<=x<=k=int(N/2)=int(5/2)=2,即0<=x<=2,list长度=N-x
4、通过观察上述步骤3发现:
(1)、N级楼梯,元素数值全为1的list长度为N,每多1个数值为2的元素,list长度就减1.如果list中有x个数值为2的元素,则list长度为N-x。
(2)、当数值2的元素个数为x个时,那么 list 数量相当于从N-x个数值全为1的元素中抽取x个元素将其元素值变为2的方法有几种。list长度=N-x 的队列 list 共有 C(N-x,x) 个。
(3)、当list中的数值为1的元素个数=0或1时,x存在最大值k(k=N/2,然后k向下取整),记为 k=int(N/2),0<=x<=k。
5、把上述过程中,累加x从0到k赋值计算出来的list数量,就是F(N)。
如上述中,N=5级楼梯走法:
x取值范围为:0<=x<=k=int(N/2)=int(5/2)=2,即0<=x<=2,list长度=N-x
(1) 当 x=0时,即list长度=5的 list 数量为:C(N-x,x)=C(5-0,0)=C(5,0)=1
(2) 当 x=1时,即list长度=4的 list 数量为:C(N-x,x)=C(5-1,1)=C(4,1)=4
(3) 当 x=2时,即list长度=3的 list 数量为:C(N-x,x)=C(5-2,2)=C(3,2)=3
所以,F(N)=F(5)=C(5,0) C(4,1) C(3,2)=1 4 3=8
综上,通过研究跨2步的次数为x(0<=x<=k)的组合数,其中k=int(N/2),就可以得出走法F(N)的值,即:
F(N)=C(N-x,x=0) C(N-x,x=1) ... C(N-x,x=k)
=C(N,0) C(N-1,1) ... C(N-k,k)
=
结果验证:
当N=1时,0<=x<=int(N/2)=0, F(N=1)=C(N=1,0)=C(1,0)=1
当N=2时,0<=x<=int(N/2)=1, F(N=2)=C(N-x,x=0) C(N-x,x=1)=C(2,0) C(1,1)=1 1=2
当N=3时,0<=x<=int(N/2)=1, F(N=3)=C(N-x,x=0) C(N-x,x=1)=C(3,0) C(2,1)=1 2=3
当N=4时,0<=x<=int(N/2)=2, F(N=4)=C(N-x,x=0) C(N-x,x=1) C(N-x,x=2)=C(4,0) C(3,1) C(2,2)=1 3 1=5
当N=5时,0<=x<=int(N/2)=2, F(N=5)=C(N-x,x=0) C(N-x,x=1) C(N-x,x=2)=C(5,0) C(4,1) C(3,2)=1 4 3=8
当N=6时,0<=x<=int(N/2)=3, F(N=6)=C(N-x,x=0) C(N-x,x=1) C(N-x,x=2) C(N-x,x=3)=C(6,0) C(5,1) C(4,2) C(3,3)=1 5 6 1=13
当N=7时,0<=x<=int(N/2)=3, F(N=7)=C(N-x,x=0) C(N-x,x=1) C(N-x,x=2) C(N-x,x=3)=C(7,0) C(6,1) C(5,2) C(4,3)=1 6 10 4=21
......
python脚本实现如下:
import math
import time
print('n级楼梯,每次跨1级或2级,有多少种走法')
'''
组合计算: 从n个元素中抽取m个元素,记为C(n,m)
'''
def fun_zuhe_jisuan(n, m):
result_n = 0
try:
if n <= 0 or m < 0 or m > n:
result_n = 0
elif m == 0:
result_n = 1
else:
fenzi = math.factorial(n) # n的阶乘
fenmu = math.factorial(m)*math.factorial(n-m)
result_n = fenzi/fenmu
except Exception as err:
print('组合: 计算从n个数中抽取m个数出来的方法,异常如下: ' str(err))
finally:
return result_n
'''
计算N级楼梯走法
'''
def fun_get_fn(n):
fn = 0 # n级楼梯走法
try:
if n == 1:
fn = 1
else:
k = int(n/2) # 数值为2元素个数最大值
for i in range(k 1): # 遍历数值为2元素个数数量
fn = fun_zuhe_jisuan(n-i, i) # fn =2级楼梯段为i的组合数
except Exception as err:
print('组合方法计算异常:' str(err))
finally:
return fn
print('3、组合方法')
for i in range(1, 30):
start_time = time.time() # 开始运行时间
fn = fun_get_fn(i)
end_time = time.time() # 运行结束时间
run_time = float(end_time-start_time)*1000 # 计算运行时间,即计算过程耗时(毫秒)
print(f'{i}级楼梯,每次跨1级或2级,有{fn}种走法,组合方法耗时:{run_time} 毫秒')
python运行结果:
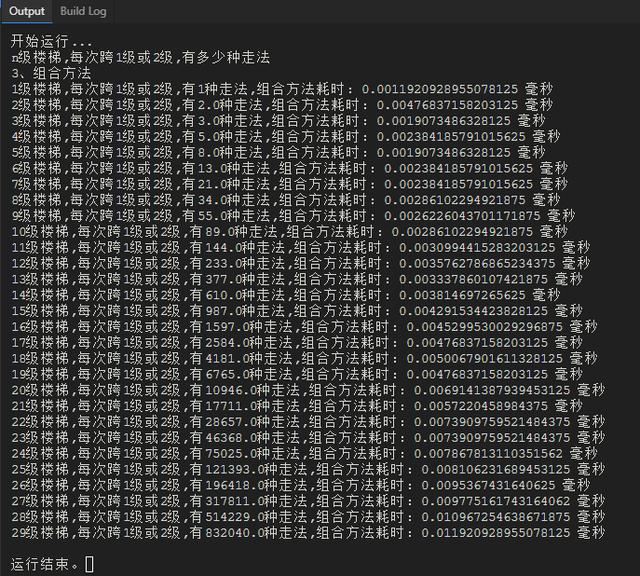
python数学组合方法计算结果
以上,便是通过数学中排列组合方式进行解题的思路、步骤、和计算结果。
,




