
和数字的几何
这是关于伦纳德·欧拉(1707–1783)系列的第二部分。您可以在这里阅读第一部分。
在我们开始探索名为欧拉身份的美丽事实之前,让我们开始一段令人惊叹的历史。
恋爱中的数字约公元前500年希腊人认为某些数字比其他数字更重要。特别是,他们知道两个具有显着特性的数字。这两个数字是220和284。
在解释这些数字为何如此有趣之前,我们需要知道什么是适当的除数。好吧,这很简单。例如,n的适当除数是小于n的自然数,将其除以n。因此,例如6的适当除数是1、2和3。现在,上面两个数字很有趣的原因是220的适当除数之和是284,而284的适当除数的总和是220.这种关系称为友善关系,而这些数字称为友善数字(友善是指朋友或情人)。实际上,过去是两个恋人采摘水果的传统,在水果的一半上写下这两个数字之一,在水果的另一半上写下另一个数字,将水果分成相应的两半,然后各消耗一块。这将"永远团结他们和他们的爱"。
希腊人认为这是非常重要的关系,但是无论他们多么努力,他们都找不到更多这样的数字。直到大约一千年前,Thābitibn Qurra才发现了两对。那时,数学的中心已经从欧洲和埃及转移到阿拉伯世界,在那里将持续近半个世纪。
Thabit的发现,以及例如但是,伊朗并没有被带到仅获知一对(希腊人)的欧洲。直到Fermat在1636年找到一对。他发现的友好数字是17,296和18,416。
在此期间,两个数学巨人之间发生了一场数学内战。即Pierre De Fermat和RenéDescartes。他们彼此憎恨,现在费马找到了两个友好的数字,因此笛卡尔必须找到另一个。在1638年,他找到了9,363,584和9,437,056对。我提醒您,这没有计算器!一定是漫长的雨天。
事实证明,费马和笛卡尔发现的这两对与Thābit发现的相同。
因此,经过2000年的明智思考和雨天,友好号的地位仅维持在三对已知的配对中……
然后,欧拉决定尝试一下。
欧拉发现58对更多的友好数字!
那太疯狂了。当然,发生的不是暴力试验和错误。取而代之的是,欧拉找到了一种依靠除数和函数的属性以及一些天才见解的方法。
你问无限多吗?没有人知道……这又是数学的奥秘之一。
最美丽的方程式欧拉在数学家中因许多事情而闻名,但是其中一种美的光芒比其他美的光芒更耀眼。尽管从技术上讲,它被称为所有数学中最漂亮的方程式,这就是所谓的恒等式。
我将以两种不同的方式解释此结果,以便读者获得直觉以及对它的数学理解(证明略图)。
首先,让我们说明一下。
欧拉的身分(1748):

那么,为什么这种关系如此美好?
好吧,首先,正如威廉·邓纳姆(William Dunham)所说:
如果要加法,则需要0,如果要乘法,则需要1,如果要进行微积分,则需要e,如果要进行几何,则需要π,如果要进行复杂分析,则需要i。这是一支梦想中的数字团队,他们全都在这个方程式中。
在解释身份之前,让我们先回顾一下并定义数字。
0和10当然是一个数字,但这是一个非常特殊的数字。这是负数和正数之间的界限,它是您不能除以的唯一数字,最重要的是,它是加法标识,这意味着x等于0时x均为x。
这看似微不足道,但实际上,这很重要,因为它是所谓的数学小组中至关重要的一部分。群论是对称的数学,但这是另一篇文章。同样,数字1当然是乘法身份。
π我们已经见过π,并且π在数学中无处不在。
从数论到概率论和三角学,但这为什么呢?
嗯,圆既与对称性有关,也与周期性有关,这些现象发生在自然界和数学中许多不同的事件中。从热量的渗透到随机游走和电磁波(或与此相关的吉他弦)的振动,再到统计分布的密度,等等。
π的定义当然是圆的周长除以其直径(任何圆,请注意),即使将其定义为比率,也不能将其写为整数的一部分。这就是我们所说的非理性(实际上是超验的)。绝对是数学巨星!
e现在,数字e呢?这个数字很难定义,但是我们会尝试一下。
首先,e是一个大约2.7182818的数字,由Euler于1748年首次发现。我无法写下所有的小数,因为它也是非理性的(和超越的)。欧拉还发现了如何计算它:

实际上,这就是Euler在1748年写的方式。今天,我们倾向于用花哨的符号来压缩它,但我不会因此而使读者厌烦。
如果您曾经做过微积分或很久以前才对某些函数求微分,那么您可能会记得微分算子有一个标识,即函数

即它具有以下属性:
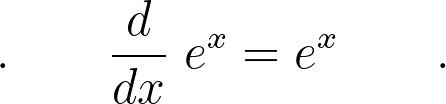
这是非常重要的,因为它一方面使我们能够求解微分方程。由于几乎所有的物理定律和系统都可以用微分方程来描述,因此它们在物理学,生物学,数学和科学中都非常重要。
因此,您可以将数字e描述为指数函数的基数,并具有以下特性:给定时刻的变化率等于该时刻的值。
i好的。那我叫多少?多年来,人们一直不接受i作为数字,但是再说一次,他们第一次出现时也不接受负数,所以我想这是成熟的问题。
在Euler时代,他们对这个数字并不十分了解。现在,对i及其使用它的功能的研究被称为复杂分析,当然,欧拉从一开始就在这个充满异国情调的新领域中处于领先地位。
与数学中的许多其他事情一样,我可以用许多不同的方式定义。一些比其他更正式。我们将坚持最简单(也是最非技术性的)的定义。i是具有以下属性的数字:

当然,没有实数满足此要求,因为如果将两个负数相乘,则会得到一个正数。我们有时称其为假想单位。
复数是a bi形式的数字,其中a和b是实数(您通常认为的数字,可以是负,零或正)。复杂分析是对复杂变量的复值函数的研究,并且(在我看来)是数学中最美丽的学科之一。
但是……你能和他们做什么?
很高兴你问。令人惊讶的是,从雷达技术到微分方程和量子力学的解决方案,等等,许多现实世界的计算都依赖于复数。
大。现在我们知道了该领域的球员。下一个问题当然是为什么欧拉的身份是真实的。
要回答这个问题,我们需要对数学运算和数字持开放的态度,并有所不同。
数字运算与几何变换之间的对偶首先,我想稍微扩展一下您的想象力。因此,想象一下数字线,即从负无穷大到无穷大,中间为零的实数。
当然,您需要足够的RAM来容纳无限大的拓扑,但是它会变得更好。现在,我们将考虑如果决定将数字行上的所有数字加2,将会发生什么。在我们的脑海中,我们将立即从上方查看整个事情。
在这种情况下,-2变为0,-1变为1,0变为2,依此类推。换句话说,整个实数线将偏移2。这种转换称为平移。
如果加0,则不会发生移位。
如果我们决定减去,即加负数怎么办?好吧,基本变换是相同的(平移),但是它是逆变换(对应于另一个方向的移动)。因此,以相同的数字进行加减则相当于在每个方向上向左和向右移动相同的量,从而使您回到开始的位置。那当然等于加0即
x-x = x (-x)= 0。
好的,所以加减实际上是关于转换的。乘法呢?
好吧,通过与上述相同的方式进行思考,您可以在脑海中看到,乘以正数实际上就是对数字行进行扩张(拉伸)。师呢?除法实际上是变相的乘法(例如,除以2等于乘以1/2),并且像以前一样是逆变换。这是关于放大或缩小。
当然,此变换的标识对应于乘以1(按比例缩放1不会执行任何操作)。
但是乘以负数又如何呢?瞧,这是一个很大的问题。这对应什么转换?
首先,我们需要记住,乘以-x实际上与先乘x然后乘-1相同。因此,当我们乘以该值时,我们首先进行x的扩容,然后进行与-1相乘的转换。
因此足以找出乘以-1的结果。
事实证明,将实数乘以-1对应于通过0的反射。您可以通过在数字行上取一个数字x并乘以-1来看到这一点。然后,您对称地降落在0的另一侧-x处。当x为负时也是如此。
请注意,现在负数乘以负数也是正数。如果您两次反思,您将回到起点。用数学语言(-1)(-1)= 1。
当我第一次发现转换和操作之间存在不同数量的双重关系时,我被美与完整性感所震惊。同样因为没有人向我解释过为什么负数乘以负数就是正数。但是这里!这是因为关于同一条线的两次反射的变换等于标识变换,即不执行任何操作的变换。此处的身份转换转换为数字和运算,对应于乘以1的动作。
事实证明,这也可以由Ring Theory领域使用称为同态的方法来解释,但这要更高级一些,后来我学到了很多。我仍然认为数字的几何形状是一种更优美的方法。
现在,我们已经解释了经典运算的实数如何与它们对应的转换配合在一起,以及它们的真实含义,但是我们缺少一个重要的转换-旋转。
让我们考虑一下。逆时针旋转存在于实线上的数字一定角度听起来很奇怪而且很危险。毕竟,如果我们不谨慎的话,我们可能会陷入一个距离我们家很远的外星世界,在我们的数字线之外,陷入另一个维度。
听起来我们必须发明一些新的怪异数字,它们存在于二维数字平面中,不是为了求解硬方程,而是为了实现转换的完整性。
顺便说一下,这在数学中经常发生。您从不同的角度看待事物,发现有趣的新事物。
好的。那么这些外星人数字的性质是什么?嗯让我们以乘以它对应于逆时针旋转90度的数字为例。
首先,我们可以通过将其乘以1来获得该有趣数字的位置,因为它应该等于自己,但也应该与将1旋转90度时得到的数字相同。
因此,这个新数字位于我们数字平面上的点(0,1),在这个新数字系统中,我们的老朋友1现在是点(1,0)。
显然,当我们乘以该数字的平方时,将旋转180度。因此,此数字的平方发送1到-1。
因此,这个神秘数的平方仅为-1。
亲爱的朋友们,我们现在推论的是,这个数字恰好是i的数字-上面的虚拟单位。因此,我是位于我们数字平面中(0,1)的数字。
因此,复数集是非常需要的自然数集,它们是开箱即用的,它们负责旋转变换。事实证明,复数a bi只不过是现在称为复平面(我们之前称为数字平面)的点(a,b)。
这意味着我们所有的数字实际上都生活在一个二维世界中,其中每个点都对应一个复数,其中包括作为(适当)子集嵌入到复平面中的实数。因此,所有实数也是复数,但并非所有复数都是实数(显然)。
这种几何视图对Euler不可用,因为它是由Caspar Wessel,Carl Friedrich Gauss等人后来首先开发的。因此,欧拉(Euler)只是将i视为具有定义它的负平方属性的数字。
现在,我们已经从这种角度理解了数字,并牢记了对偶性,我们只需要一种成分就可以直观地了解Euler的身份。
尽管在揭示这种成分之前,我们需要知道什么是弧度。想一想,为什么一圈有360度?
事实证明,这是巴比伦人及其十六进制数制的遗留物。完全不尊重数字60,但是它是任意的(不是完全任意的,但这是一个漫长的故事),数学家也不喜欢。事情应该是自然的。
因此,我们以另一种方式计算"度"。全部涉及半径为1的归一化圆,即所谓的单位圆。该圆定义了三角函数,即余弦,正弦,切线,割线等,因此使用它定义度数是很自然的。
这个想法是,我们没有选择一个任意的数字作为"整个方向",而是简单地选择了单位圆的周长。因此360度对应于2π弧度,180度对应于π弧度,依此类推。
现在我们准备好最后的食材了。
以下是一个事实,我们将稍作概述,但现在,我们仅在此处进行说明:
当我们将任何复数z(包括实数还记得吗?)乘以该数时

然后将结果旋转z弧度θ弧度。
现在,我们准备通过对数字及其相互运算的新理解再次查看欧拉的身份。已经有一段时间了,让我们重温一下,但是这次写的有点不同。

那么这是什么意思呢?
好吧,真的很简单。我们知道,左侧只是说:"以π弧度旋转" 180度还记得吗?右边说:"反射数字0"。
因此,欧拉的身份在说什么:
180度的旋转与通过0的反射相同。
简单,美丽,优雅!
好的,现在我们可以从几何学的角度理解它,这当然很好,因为现在我们有了一些与方程相关联的图像,但这并不是证明。这几乎是一个证明,但我们从未展示过数字e与与其关联的复数角度(称为其自变量)之间的关系。另外,我想向您展示欧拉如何证明自己的身份。
欧拉以更一般的结果(也是一个恒等式)表示角度和指数函数之间的关系,即
欧拉公式(1748)

在证明这一点之前,我们先坐下来欣赏一下这个结果。
首先,这意味着指数函数是周期性的!绘制其图形时可能看起来不像,但这是因为其周期是虚构的。周期当然是2πi,因为余弦和正弦都具有周期2π(请注意,我们所谈论的三角函数是用弧度而不是您在高中学习的度数定义的)。
让我们快速浏览一下Euler的证明。
您可能从上一篇文章中回想起我们可以将某些函数编写为称为泰勒级数的幂级数。这里是:

首先,他在Maclaurin系列中写出指数。
然后他把我从括号里拉出来。请注意,右括号内的级数是交替出现的,因为如果将虚数单位提高为4n形式的数字,则得到1、4n 1得到i,4n 2得到-1、4n 3得到-一世。
此后,他将括号内的两个系列(当然是)识别为麦克劳林的余弦和正弦序列(当然是)。从本系列第一部分中的巴塞尔问题证明,即数字无穷大(伦纳德·欧拉),您可能会认识到这种表示形式中的正弦函数。
为了解释指数函数和角度之间的关系,可将一个复数想象为坐标为(a,b)的复平面上的一个点。该数字可以写为a bi,并且距原点有一段距离。我们将此距离称为长度(或模量)r。现在,与实线的角度如何?
好吧,如果我们从点(a,b)向下到与假想轴平行的实轴(实数线)画一条线,并且还从我们的点到原点画一条线,我们会形成一个直角三角形。原点处的角度正好是复数a bi的参数,在我们的转换语言中,它是该数乘以其他数时所旋转的角度。

为了找到复数的自变量(或角度),我们从三角学中记得,当斜边的长度为r时,角度的正弦值乘以r就是对边的长度,角度的余弦值乘以r是相邻边的长度。
换句话说,在我们的复数a ib中,我们有a = rcos(θ)和b = rsin(θ)。所以

我们在上一个等式中使用了欧拉的身分换句话说:任何复数a bi都可以通过指数函数根据其自变量和模数以这种极性表示法来写。
但是,欧拉更普遍的身份如何证明他的"梦之队"方程式呢?
好吧,如果x =π,则正弦项消失(变为0),而余弦项变为-1,因为pi弧度为180度。
这最终证明了他美丽的方程式,但有些绕了弯。
有人说欧拉是有史以来最伟大的数学,有人说高斯,但最后没关系。重要的是我们确实站在巨人的肩膀上。
在一开始就把趣味数字告诉轶事的方式极大地受到了威廉·邓纳姆(William Dunham)令人敬畏和丰富多彩的教导的启发。
在本系列的下一部分中,我们将讨论Euler提出的一些美丽见解,这些见解导致了数学的崭新领域-拓扑。
阅读欧拉,阅读欧拉。他是我们所有人的主人
〜皮埃尔·西蒙·拉普拉斯
(本文由闻数起舞翻译自123 Followers的文章《The Most Beautiful Equation in the World》,转载请注明出处,原文链接:https://kaspermuller.medium.com/the-most-beautiful-equation-in-the-world-5ab6e49c363)
,




