所谓二次函数与矩形存在性问题,即在二次函数中确定动点位置,使其与其他点等构成矩形,本文将对题型构造及解决方法作简单介绍.首先关于矩形本身,我们已经知道:矩形的判定(1)有一个角是直角的平行四边形;(2)对角线相等的平行四边形;(3)有三个角为直角的四边形.

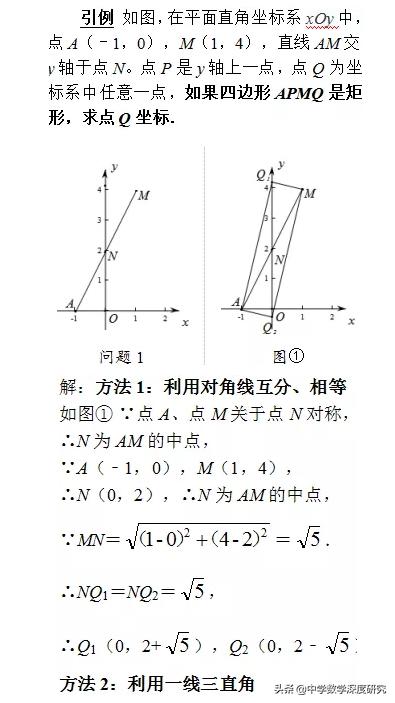
第一步:先画草图。因为题目已经明确四边形顶点的顺序,所以可以得知A,M为矩形相对的两个顶点。第二步:求点坐标,可以直接通过对角线相等计算长度。
解题模型探究1.铺垫知识
铺垫1:直角三角形存在类问题的几何作图方法
已知点C为直线上一动点,请问是否存在点C使得△ABC为直角三角形,如果存在,请画出示意图.

图1是指以点A为直角顶点时对应的C点;图2是指以点B为直角顶点时对应的C点;图3是指以AB为直径和直线相交时对应的C点.上述作图方法我们简称为"一圆两垂直"
铺垫2:直角三角形存在类问题的解题策略详情请参考"二次函数与直角三角形存在类问题"
铺垫3:平行四边形顶点坐标公式
根据平行四边形的性质对角线互相平分,可以知道点O为线段AC和线段BD的中点。
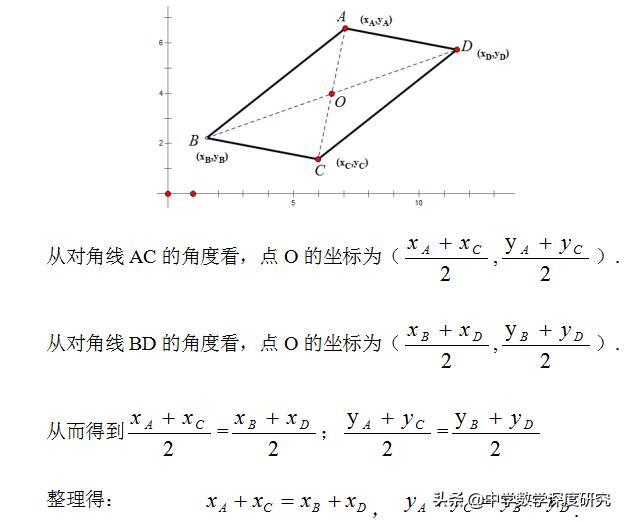

(AC为对角线时)
因此在矩形存在性问题最多可以有3个未知量,代入可以得到三元一次方程组,可解.确定了有3个未知量,则可判断常见矩形存在性问题至少有2个动点,多则可以有3个.

2.题型分类:
(1)2个定点 1个半动点 1个全动点;
(2)1个定点 3个半动点.
思路1:先直角,再矩形
在构成矩形的4个点中任取3个点,必构成直角三角形,以此为出发点,可先确定其中3个点构造直角三角形,再确定第4个点.对"2定 1半动 1全动"尤其适用.
引例:已知A(1,1)、B(4,2),点C在x轴上,点D在平面中,且以A、B、C、D为顶点的四边形是矩形,求D点坐标.


【小结】这种解决矩形存在性问题的方法相当于在直角三角形存在性问题上再加一步求D点坐标,也是因为这两个图形之间的密切关系方能如此.
思路2:先平行,再矩形
当AC为对角线时,A、B、C、D满足以下3个等式,则为矩形:

其中第1、2个式子是平行四边形的要求,再加上式3可为矩形.表示出点坐标后,代入点坐标解方程即可.无论是"2定1半1全"还是"1定3半",对于我们列方程来解都没什么区别,能得到的都是三元一次方程组.
引例:已知A(1,1)、B(4,2),点C在x轴上,点D在平面中,且以A、B、C、D为顶点的四边形是矩形,求D点坐标.

【小结】这个方法是在平行四边形基础上多加一个等式而已,剩下的都是计算的故事.

1.构造对角线互相平分且相等得矩形
例1(2019南充中考题,有删减)如图,抛物线y=ax² bx c与x轴交于点A(-1,0),点B(-3,0),且OB=OC.
(1)求抛物线的解析式;
(2)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m 4.点D是抛物线上M、N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值;
②点D关于点E的对称点为F,当m为何值时,四边形MDNF为矩形.


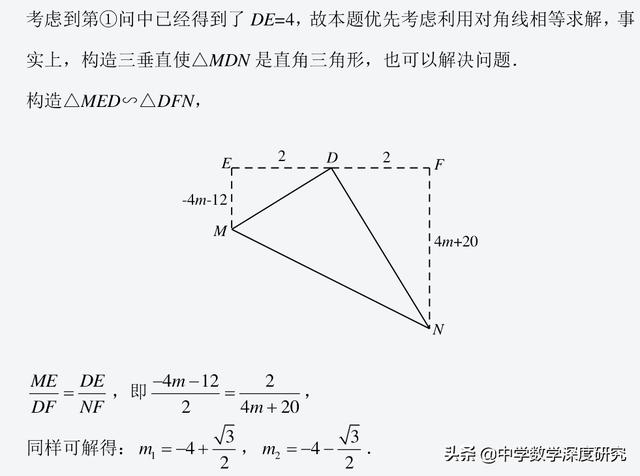
2.构造直角得矩形
例2(2018铁岭中考题,有删减)如图,抛物线y=-x² bx c交x轴于点A,B,交y轴于点C.点B的坐标为(3,0)点C的坐标为(0,3),点C与点D关于抛物线的对称轴对称.
(1)求抛物线的解析式;
(2)若点P为抛物线对称轴上一点,连接BD,以PD,PB为边作平行四边形PDNB,是否存在这样的点P,使得平行四边形PDNB是矩形?若存在,请求出tan∠BDN的值;若不存在,请说明理由.



以二次函数为背景的矩形存在性问题,需要在复杂的问题中牢牢把握核心问题,确定求动点坐标,把矩形问题转化为直角三角形存在性问题,画图,并求解。这样可以让学生清楚问题的来龙去脉,以及相关图形的组合。
第一步:分类讨论。分清具体边为对角线,还是为矩形的边。第二步:作图。可以利用对角线互分,相等;边平移,作垂线。第三步:利用直角三角形的性质求点坐标(转化为直角三角形存在性问题,通过一线三直角,斜边上的中线等于斜边的一半解决)体会一线三直角方法更好,优化方法。
,




