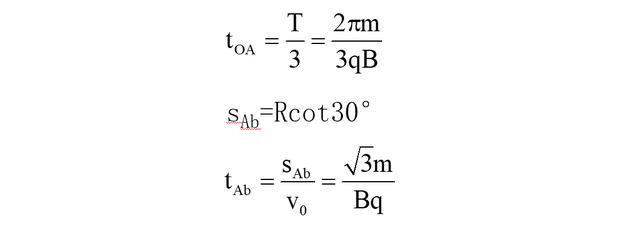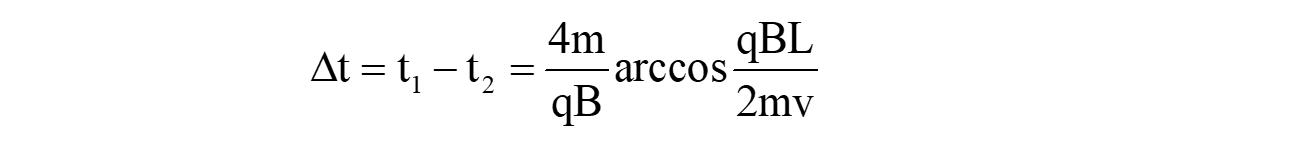带电粒子(不计重力)垂直射入匀强磁场,粒子的运动轨迹是圆周或圆弧.这类问题是常见的典型的力学、磁场知识结合的综合题,在高考中多次考查,是考试的难点.
求解这类问题的关键是:定圆心画出轨迹,求出半径,确定圆心角等.其中解决带电粒子在有界磁场中的运动、确定圆心是解题的难点.
本文就确定圆心的三种比较典型的方法做深入归纳总结

适用情况:如果已知带电粒子的出射速度和入射速度方向,分别作出过入
射点和出射点速度方向的垂线,两垂线的交点便是圆心.如图所示

例题分析
【题目】电视机的显像管中,电子束的偏转是使用磁偏转技术实现的.电子束经过电压为U的加速电场后,进入一圆形匀强磁场区,如图所示,磁场方向垂直于圆面.磁场区的中心为O,半径为r.当不加磁场时,电子束将通过O点而达到屏幕的中心M点.为了让电子束射到屏幕边缘P,需要加磁场,使电子束偏转一已知角度θ
【问题】此时磁场的磁感应强度为多大?(已知电子质量为m,电荷量为e)

【分析】分别作入射点和出射点速度方向的垂线,其交点为电子做匀速圆周运动的圆心C,以v表示电子进入磁场时的速度,则

根据以上可以解出

核心要点:已知入射与出射速度的位置与方向,做出垂线交点可得圆心
第二种方法:速度垂线与角平分线交点定圆心
适用情况:如果已知带电粒子的出射速度和入射速度方向,则入射速度方向的延长线和出射速度方向的反向延长线夹角的角平分线与入射速度垂线的交点就是圆心.如图所示.
例题分析
【题目】一质量为m、带电量为q的粒子,以速度v0从O点沿y轴正方向射入磁感应强度为B的一圆形匀强磁场区域,磁场方向垂直于纸面,粒子飞出磁场区域后,从b处穿过x轴,速度方
向与x轴正方向夹角为30°,不计重力.
【问题】(1)圆形磁场区域的最小面积;(2)粒子从O点进入磁场区域到达b点所经历的时间及b点坐标.
【分析】(1)由于粒子沿y轴正方向射入,所以圆心必在x轴上,反向延长b处的速度方向与y轴相交于C点,作∠OCA的角平分线与x轴相交于O′点,过O′点作bC的垂线,垂足为A点.则O′A=O′O=R,所以,以OA为直径的圆的磁场区域面积最小.设圆形磁场区域的半径为r.由牛顿第二定律得:
根据图中几何关系可知
最小面积为
(2)粒子从O点沿圆弧到A点,所经历的时间
所以粒子从O点进入磁场区域到达b点所经历的时间为
b点横坐标为
核心要点:已知入射速度位置及方向,出射方向已知,但是不知道出射点在哪里,可以用速度垂线及角平分线过圆心的方法确定圆心
第三种方法:速度垂线与弦的垂直平分线过圆心
适用情况:如果已知带电粒子的入射速度方向和做圆周运动轨迹的一条弦,先作出过入射点速度方向的垂线,然后作弦的垂直平分线,两垂线的交点便是圆心.
例题分析
【题目】如图,虚线MN是一垂直纸面的平面与纸面的交线,在平面右侧的空间存在磁感应强度为B的匀强磁场,方向垂直纸面向外,O是MN上的一点,从O点可以向磁场区域发射电荷量为 q、质量为m、速率为v的粒子,粒子射入磁场时的速度可在纸面内各个方向.已知先后射入的两个粒子恰好在磁场中给定的P点相遇,P到O点的距离为L,不计重力及粒子间的相互作用.
【问题】(1)求所考查的粒子在磁场中运动的轨道半径;(2)求这两个粒子从O点射入磁场时的时间间隔.
【分析】(1)设粒子在磁场中做圆周运动的轨道半径为R,
洛伦兹力充当向心力,由牛顿第二定律
解出
(2)如图所示,为两粒子在匀强磁场中运动的轨迹图. 作图方法是:作OP的垂直平分线,分别过入射点O作入射速度1、2的垂线.两垂线与垂直平分线的交点分别为O1、O2,则O1、O2为圆心,粒子1转过的角度为∠OO1P=π θ,粒子2转过的角度为∠OO2P=π-θ两粒子在磁场中运动的周期均为
粒子1从O点运动到P点所用的时间为:
粒子2从O点运动到P点所用的时间为:
两粒子射入的时间间隔:
又因为
则有
时间间隔为
核心要点:已知入射速度位置及方向,出射速度位置,但是不知道出射速度方向,可以根据速度垂线与弦的垂直平分线过圆心确定圆心
我是方哥
一个不太出名但是又有点理想的物理老师
点个关注,你我缘分就此开始
,