容斥原理在高中叫做“集合问题”,其难度中等且做题技巧性强,深受命题人喜爱,因此是行测考试中经常出现的一类题型。
纵观联考真题,容斥问题考的并不多,2009-2014年六年12套联考真题,总共出了2道容斥问题,分别是2012年421联考和2014年412联考。并不是说容斥问题出的少我们就可以忽略了,在2014年、2015年国考,以及2014年广东、浙江、河北等单独命题的省考中,容斥问题都曾出现,根据以往经验,国考一直是联考的风向标,且各省市相互借鉴,我们在复习备考联考时,容斥问题依然是重要的内容,掌握容斥问题的题型特征和做题方法是十分必要的。
一、容斥问题题型分类
第一类题型:两集合容斥原理公式:|A UB|=|A| |B|-|A∩B|=总个数- 两者都不满足的个数
第二类题型:(1)三集合容斥原理标准公式:|A UBUC|=|A| |B| |C|-|A∩B|-|B ∩C|-|C∩A| |A∩B∩C|=总个数- 三者都不满足的个数
(2)三集合容斥原理变形公式:|A UBUC|=|A| |B| |C|-仅满足两个条件的情况数|-2|A∩B∩C|=总个数- 三者都不满足的个数
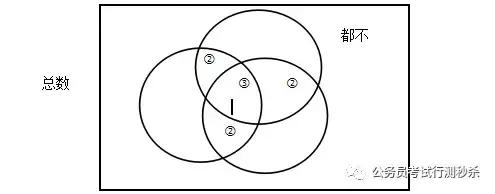
注意 ② :仅满足2种情况的个数
③ :同时满足3种情况的个数
第三类题型:图示类题型,通常是在套用公式条件不足时采用,一般是文氏图,标数时从内向外标。
二、历年联考真题范例解析:
例1:(2012.421联考)54.某公司招聘员工,按规定每人至多可投考两个职位,结果共42人报名,甲、乙、丙三个职位报名人数分别是22人、16人、25人,其中同时报甲、乙职位的人数为8人,同时报甲、丙职位的人数为6人,那么同时报乙、丙职位的人数为:
A.7人B.8人
C.5人D.6人
解析:三集合容斥原理。根据公式:总个数- 三者都不满足的个数=|A UBUC|=|A| |B| |C|-|A∩B|-|B∩C|-|C∩A| |A∩B∩C|。设同时报乙丙职位的人数为x。理解题意之后代入公式:42-0=22 16 25-(8 6 x) 0,得到同时报乙丙职位的人数x=7。因此,本题答案选择A选项。
例2:某单位利用业余时间举行了3次义务劳动,总计有112人次参加。在参加义务劳动的人中,只参加1次,参加2次和3次全部都参加的人数之比为5:4:1。问该单位共有多少人参加了义务劳动?
A.70B.80
C.85D.102
解析:根据题目条件,假设参加1次、2次、3次的人数分别为5X,4X,X。文氏图图示法,所以得知5X 4*2X 3*X=112,X=7,所以一共参加劳动的人数为70人。因此,本题答案选择A选项。
以上两道例题是联考中的真题,为了便于广大广大考生掌握容斥问题的这几类题型和做题技巧,故在此增加两道例题。
例3:某班有60人,参加物理竞赛的有30人,参加数学竞赛的有32人,两者都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人?
A.28人B.26
C.24人D.22人
解析:根据两集合容斥原理标准公式,|A UB|=|A| |B|-|A∩B|=总个数- 两者都不满足的个数,设同时参加物理、数学竞赛的有X人,代入公式30 32-X=60-20,X=22。因此,本题答案为D选项。
例4:某高校对一些学生进行问卷调查。在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备选择两种考试参加的有46人,不参加其中任何一种考试的有15人。问接受调查的学生共有多少人?( )
A.120B.144
C.177D.192
解析:根据三集合容斥原理的变形公式,|A UBUC|=|A| |B| |C|-仅满足两个条件的情况数|-2|A∩B∩C|=总个数- 三者都不满足的个数。设接受调查的学生共有X人,代入公式63 89 47-46-2×24=X-15 ,X=120,因此,本题答案为A选项。
综上,要想真正掌握容斥问题,不仅需要公式,还需要牢固掌握题目特征,多加练习,根据题目中给定的条件,灵活运用这些方法。
更多内容进入国考大师·刷课君或加入2017国考笔试交流群:203357342
,




