精度控制总原则
选项最小差距决定计算允许的误差!
选项最小差距决定计算允许的误差!
选项最小差距决定计算允许的误差!
这就决定了,我们计算之前永远都要先看选项,再决定计算方式。
选项差距在10%以上的题目,都是送分题,基本不需要动笔,大部分都可以直接瞪出来。
一般来说,计算误差小于选项最小差距的1/3,足以保证计算结果的可靠。这里说的选项间的差距是相对差距,不是绝对差距,比如1%和2%,它们之间的绝对差距是1个百分点,非常小,但是相对差距是50%,属于非常大的差距了。选项是1%、2%、3%、4%,明显要比选项是89%、90%、91%、92%好算的多。
另外,这里的1/3不是定死的,只是说小于1/3很可靠,但是比1/3稍大点,也比较可靠,但是如果接近1/2就不大可靠了,如果超过1/2就很不可靠了。在实际的考试中,不需要严格按照1/3来控制误差,大体估量即可。
举例:
A和B是两个100左右的数,比如107/(1 6.3%)和98/(1-3%)
题干是A×B,选项是8000,9000,10000,11000,误差在10%左右,那么我们在对A和B进行化简的过程中,误差需要控制在3%以内,除法同理。但是如果选项是9800,9900,10000,10100,相对差距在1%左右,那么我们我们在对A和B进行化简的过程中,误差需要控制在0.3%以内,除法同理。
但是减法运算和乘除法又有所不同。
题干是A-B=C,让我们求C,这时候计算精度取决于选项之间的绝对差距。如果选项之间的绝对差距相较于两个相减的数,算是比较大的,那么我们计算的过程中就可以对A和B比较大的简化,但是如果选项之间的差距相较于两个相减的数,算是非常小的,我们就需要比较精确地计算。
举一个极端点的例子:
10001-10000=?A.1 B.2 C.3 D.4
选项之间相对差距很大,但是绝对差距只有1,相对于两个相减的量,很小,我们在对两个数进行化简的过程中,万分之一的误差,都会对结果造成巨大影响。
但是如果上述例子换成:
12000-10000=?A.1000 B.2000 C.3000 D.4000
那么我们在对两个相减数进行化简的过程,就可以适当地放开手脚了。
误差控制时,乘法和加法,要一增一减,除法和减法要同增同减,这样产生的误差可以互相抵消一部分。
比如:A×B,我们要使得A增大1%,就相应的使得B减小1%,误差可以极大地抵消。
A B,我们要使得A增大1%,这时候需要观察AB之间的倍数关系,B相应的减少若干倍的1%。
A÷B,我们要使得A增大1%,就相应的使得B增大1%,才可以使得式子的值不发生改变。
A-B,我们要使得A增大1%,这时候同样需要观察AB之间的倍数关系,B相应的增大若干倍的1%。
【例】2020年12月北京公务员考试
材料:2016年公有制企事业单位中女性专业技术人员1480万人,所占比重达47.8%;其中女性高级专业技术人员161万人,所占比重38.3%。
问题:2016年公有制企事业单位中,高级专业技术人员占专业技术人员的比重约为:
A.7.5% B.13.6% C.22.9% D.36.1%
【解析】B。选项差距较大,简单估算即可,

,乘号前面略大于10%,后面接近50/40,所以整体比12.5%稍大,只能选B。
【例】2019年山东省考114题:
材料中给出“每千人口医疗卫生机构床位数由2016年5.37张增加到2017年的5.72张”,“2016、2017年床位数分别为741万张、794万张”。问从所给数据资料中可以推算,2017年末全国人口总数比2016年末增加量最接近:
A.741万 B.822万 C.895万 D.988万
【解析】B。算式为794万×1000/5.72-741万×1000/5.37,一个14亿左右的数减去另一个14亿左右的数,选项是几百万,而选项间的差距只有几十万。这时候,我们对这两个14亿左右的数进行任何化简,都会对结果造成巨大影响,所以只能精算。
【例】 2021年公务员联考
材料:(2019年一季度),资产管理业务净收入57.33亿元,同比下降15.43%……利息净收入69.04亿元,同比增长4.94%。
题目:2018年第一季度,131家证券公司资产管理业务净收入与同期利息净收入相比约:
A.少了2.0亿元
B.多了2.0亿元
C.少了3.1亿元
D.多了3.1亿元
【例】(166 2838.2 8490.4)/16469.7=?
A.68% B.70% C.75% D.80%
【解析】B。选项间最小差距是2个百分点,大概占70%的3%左右,根据我们的1/3原则,我们对算式进行化简的过程中,只要误差小于1%,都是可以的。166和2838.2相加,大概是3000,3000和8490.4相加,大概是11500,下面的16469可以直接看成165,以上所有近似产生的误差均在1%以内,足以保证计算结果的准确。115/165=23/33,懒得算这个除法的话,可以用33×70%=23.1,说明这个除法的结果非常接近70%,故答案选B。
【例】(2019年1103辽宁公务员考试)2018年市场主体343.8万户,同比增长8.2%,增速增加1.1个百分点;企业为90.7万户,同比增长12%,增速回落2.9个百分点。则2016年各类市场主体中企业占比约为:
A.24% B.26% C.27% D.28%
【解析】选项间最小差1个百分点,相对于百分之二十几,大概存在4%的差距,根据1/3原则,我们计算中,1%以内的替换是没问题的。由题意知,2017年相当于2016年,市场主体增加了8.2%-1.1%=7.1%,企业增长了12% 2.9%=14.9%,则18年比16年,市场主体增长了8.2% 7.1% 8.2%×7.1%≈16%,企业增长了12% 14.9% 12%×14.9%≈28.8%,则:
算式=

,前面的分式稍微大于25%,后面的稍微小于1,故相乘应该在25%附近,锁定AB。原算式≈
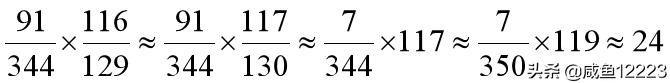
,故选A。整个计算过程,我近似了很多步,但是每一步误差都非常小,满足1/3原则的要求,所以计算结果才是可靠的。
【例】(2019年1103辽宁公务员考试)2018年工业主营业务利润1460.3亿元,同比增长41.8%,收入26489.8亿元,同比增长15.8%。 则2017年规模以上工业主营业务利润率约为:
A.4.3% B.4.5% C.4.9% D.5.2%
【解析】算式=

,选B。
最后一步是因为对数字敏感,看到265想到2.66,想到8/3。整个估算过程,每一步误差都很小,保证了计算的准确。那么如何判断误差足够小了呢?选项之间最小差距是0.2%,大概占百分之四点几的4%左右,所以同样,1%内的替换是没问题的。
,