已知:如图,在 Rt △ABC 中 , ∠C = 90° ,a , b , c , 分别为 ∠A , ∠B , ∠C 所对应的边,⊙O 为 Rt △ABC 的内切圆 ,半径为 r 。
求证:2r = a b - c 。
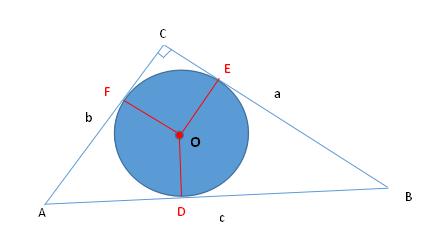
图
证法一、(切线长的性质):
过 ⊙O 分别作 OF⊥AC , OE⊥BC , OD⊥AB 垂足分别为 F 、E、D ,则有 OF = OE = OD = r
在 Rt △AOF 和 Rt △AOD 中 由勾股定理得 :
AO^2 = AF^2 OF^2 = AD^2 OD^2
所以可得: AF = AD
同理可得:BD = BE
在 Rt △ABC 中
∵ a = CE EB = r BE ,
b = CF FA = r FA ,
c = AD DB 。
∴ c = b - r a - r = b a - 2r
∴ 2r = a b - c
证法二、(等积法)
连接 OA , OB , OC
S△ABC = 1/2 ab
S△OAB = 1/2 rc
S△BOC = 1/2 ra
S△COA = 1/2 rb
∵ S△ABC = S△OAB S△BOC S△COA
∴ 1/2 ab = 1/2 rc 1/2 ra 1/2 rb 即 ab = r ( a b c )
∵ 在 Rt △ABC 中 a^2 b^2 = c^2
∴ a^2 b^2 2ab = c^2 2ab 即 ( a b )^2 - c^2 = 2ab
∴ ( a b c)( a b - c ) = 2ab = 2r ( a b c )
∴ 2r = a b - c
,




