下面使用动态规划来实现简单的正则表达式匹配。题目如下:
假设?可以匹配任意的一个字符,*可以匹配0到任意个字符,正则表达式只能由数字,英文字母、?和*组成,字符串由英文字母和数字组成,编写一个程序,给定一个满足上述规则的正则表达式和字符串,返回正则表达式是否匹配该字符串。
以下是匹配的例子:

下面看看代码如何写。
用pattern = "hel?o"和 sentence = "hello"进行尝试:

发现pattern[0] = sentence[0],则i和j分别 1,继续判断,直到i=3和j=3,如下图所示:
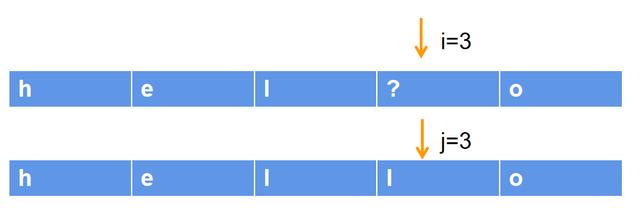
此时pattern[3] != sentence[3],但由于pattern[i]此时的值为?,可以匹配任意一个字符,因此认为仍然匹配,i和j分别 1,继续往下匹配。
定义表达式dp(i,j)为pattern[i:]和sentence[j:]是否匹配。从上述分析可以看出,如果
pattern[i] == sentence[j] 或者 sentence[j] == "?",则 dp[i][j] = dp[i 1][j 1]。
主要的困难在于*的处理。假设pattern="***bc",sentence="abc",那么,对于第一个*号,可以有以下4种情形:
情形1:不匹配任何字符

情形2:匹配第一个字符
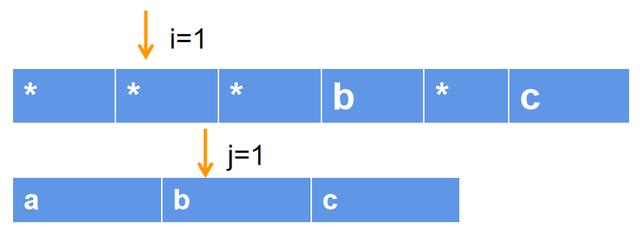
情形3:匹配前二个字符:

情形4:匹配前三个字符:

经过上述分析,可以得出结论:
dp[i][j] = U(dp[i 1][k]), k=j....N。 其中只要有任意一个dp[i 1][k]为True,则
dp[i][j] = True
代码编写如下:
def simple_regex(mod,s,i,j):
if i<len(mod) and j<len(s) and (mod[i] == s[j] or mod[i] == "?"):
return simple_regex(mod,s,i 1,j 1)
elif i == len(mod):
return j == len(s)
elif mod[i] == "*":
for k in range(j,len(s) 1):
if simple_regex(mod,s,i 1,k):
return True
return False
print(simple_regex("a*b*c*d****e","athis is a boy and cow and welcome",0,0))
print(simple_regex( "*p*","help",0,0))
print(simple_regex( "*p*","papa",0,0))
print(simple_regex( "*p*","a",0,0))
print(simple_regex( "*p*","p",0,0))
print(simple_regex("he?p","p",0,0))
print(simple_regex("he?p","help",0,0))
print(simple_regex("he?p","heap",0,0))
print(simple_regex("he?p","healp",0,0))
print(simple_regex("*bb*","babbbc",0,0))
print(simple_regex("*bb*p","babbbc",0,0))
print(simple_regex("*bb*","babbbc",0,0))
print(simple_regex("***bb*","b",0,0))
程序输出:
True
True
True
False
True
False
True
True
False
True
False
True
False
按照动态规划的思路,增加缓存,同时将
for k in range(j,len(s) 1):
if simple_regex(mod,s,i 1,k):
替换成递归的实现以提升效率,代码如下:
pattern ="t*b*c*d****e"
sentence = "this is a boy and cow and welcome"
cache = [[-1 for i in range(len(sentence) 1)] for j in range(len(pattern) 1)]
def simple_regex(mod,s,i,j):
if not (cache[i][j] == -1):
return cache[i][j]
cache[i][j] = False
if i<len(mod) and j<len(s) and (mod[i] == s[j] or mod[i] == "?"):
cache[i][j] =simple_regex(mod,s,i 1,j 1)
elif i == len(mod):
cache[i][j] = j == len(s)
elif mod[i] == "*":
cache[i][j] = simple_regex(mod,s,i 1,j) or (j<len(s) 1 and simple_regex(mod,s,i,j 1))
return cache[i][j]
print(wild_char(pattern,sentence,0,0))
解释下上述代码。
第13行,当mod[i]==‘*’时,我们将循环写成了递归形式。simple_regex(mod,s,i 1,j)表示*号不匹配任何字符。simple_regex(mod,s,i,j 1)表示*号匹配一个字符后,进入下一次递归调用。通过这两个递归组合就完成了
for k in range(j,len(s) 1):
if simple_regex(mod,s,i 1,k):
达到的效果。
,




